一 : 17高三立体几何专题练习(含答案)

立体几何专题练习卷

一、填空题（本大题满分56分，每小题4分） 1．正方体

ABCD?A1B1C1D

的棱长为a，则异面直线AB1与BC1所成的角的大小

是__________．

2．已知某铅球的表面积是484?cm，则该铅球的体积是___________cm．

2

2

3．若圆锥的侧面积为20?，且母线与底面所成的角为

arccos

4

5，则该圆锥的体积

为___________．

ABCD?A1B1C1D1中，若AB?2,BC?1,AA1?3，则BC1与平面4．在长方体

BB1D1D所成的角?可用反三角函数值表示为??____________．

OO

6371318'，BA12127'5．若取地球的半径为米，球面上两点位于东经，北纬OO

位于东经12127'，北纬255'，则A、B两点的球面距离为_____________千米

(结果精确到1千米)．

2

6．已知圆锥的母线长为5cm，侧面积为15? cm，则此圆锥的体积为3cm__________．

7．若圆锥的底面半径和高都是2，则圆锥的侧面积是_____________． 8．如图，是一个无盖正方体盒子的表面展开图，A、B、C为其上的三个点，则

在正方体盒子中，?ABC?

____________.

第9题

9．一个圆柱形容器的轴截面尺寸如右图所示，容器内有一个实心的球，球的直

径恰等于圆柱的高.现用水将该容器注满，然后取出该球（假设球的密度大于水

且操作过程中水量损失不计），则球取出后，容器中水面的高度为__________cm. （精确到0.1cm）

10．如图，用铁皮制作一个无盖的圆锥形容器，已知

该圆锥的母线与底面所在平面的夹角为45?，容器的

高为10cm．制作该容器需要铁皮面积为

__________cm2．（衔接部分忽略不计，结果保留整

数）

11．如图，圆锥的侧面展开图恰好是一个半圆，则该圆锥的

母线与底面所成的角的大小是

__________ .

??

12．如右下图，?ABC中，?C?90，?A?30，BC?1．在三角形内挖去半圆

（圆心O在边AC上，半圆与BC、AB相切于点C、M，与AC交于N），则图中阴影部分绕直线AC旋转一星期所得旋转体的体积为__________ ．

13．如图所示，以圆柱的下底面为底面，并以圆柱的上底面

圆心为顶点作圆锥， 则该圆锥与圆柱等底等高。若圆锥的轴截面是一个正三角形，则圆柱的侧面积与圆锥的侧面积之比为__________

14．一个圆锥形的空杯子上面放着一个球形的冰淇淋，圆锥底的直径与球的直径相同均为10，如果冰淇淋融化后全部流在空杯子中，并且不会溢出杯子，则杯子的高度最小为____________．

二、选择题（本大题满分20分，每小题5分） 15．如图，P为正方体

DA1

P

DA

C1

ABCD?A1B1C1D1的中心，△PAC在该正方体各个面上

C1

的射影可能是（ ）

A. (1)、(2)、(3)、(4) B.(1)、(3) C.(1)、(4) D.(2)、(4) 16．给出下列命题：(1)三点确定一个平面；(2)在空间中，过直线外一点只能作一条直线与该直线平行；(3)若平面?上有不共线的三点到平面?的距离相等，

(1)(2)

(3)

(4)

则?//?；(4)若直线a、b、c满足a?b、a?c,则b//c.其中正确命题的个数是 ( )

A．0个 B．1个 C．2个 D．3个

17. 已知长方体的表面积是24cm，过同一顶点的三条棱长之和是6cm，则它的对

2

角线长是（ ）

B. 4cm

C.

D.

18．用一个平面去截正方体，所得截面不可能是 （ ）．

（A） 平面六边形； （B）菱形； （C）梯形； （D）直角三角形

三、解答题（本大题满分74分）

19．（满分14分）本题共有2小题，第1小题满分7分，第2小题满分7分．

如图：三棱锥P?ABC中，PA?底面ABC，若底 面ABC是边长为2的正三角形，且PB与底面ABC

?

所成的角为3．若M是BC的中点，求： （1）三棱锥P?ABC的体积；

A AC（2）异面直线PM与所成角的大小（结果用反三角函数值表示）．

20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分． 如图，在四棱锥P?ABCD中，底面ABCD是

边长为2的菱形，?ABC?60，PA?平面ABCD，

PC与平面ABCD所成角的大小为arctan2，M为 PA的中点．

C

D

（1）求四棱锥P?ABCD的体积；

（2）求异面直线BM与PC所成角的大小（结果用 反三角函数表示）．

21. （本题满分14分）第1小题8分，第2小题6分.

如图，正四棱锥P?ABCD底面的四个顶点A,B,C,D在球

O 的同一个大圆上，点P在球面上，且已知(1)求球O的表面积；

VP?ABCD?

16

3.

P

(2)设M为BC中点，求异面直线AM与PC所成角的大小.

22．（本题满分16分，第1小题7分，第2小题9分）

如图，在直三棱柱ABC?A1B1C1中，

C1

A1

B1

C1C?

A?C

2B??ACB?90?. ，C

（1） 下图给出了该直三棱柱三视图中的主视图，请据此画出它的左视图和俯视图；

（2） 若P是AA1的中点，求四棱锥B1?C1A1PC的体积.

C

B

A

第22题图

23．（本题满分16分，第1小题8分，第2小题8分） C1

A1

B1

如图，在直三棱柱ABC?A1B1C1中，CC1?AC?BC，

?ACB?90?，P是AA1的中点，Q是AB的中点.

P

（1）求异面直线PQ与B1C所成角的大小；

1

（2）若直三棱柱ABC?A1B1C1的体积为2，求四棱锥

A

B

C?BAPB1的体积.

立体几何专题练习卷答案

的棱长为a，则异面直线AB1与BC1所成的角的大小

一、填空题（本大题满分56分，每小题4分） 1．正方体

ABCD?A1B1C1D

是__________． 答案：60?

2．已知某铅球的表面积是484?cm，则该铅球的体积是___________cm． 答案：

2

2

4?1331?

3

3．若圆锥的侧面积为20?，且母线与底面所成的角为

arccos

4

5，则该圆锥的体积

为___________． 答案：16?

ABCD?A1B1C1D1中，若AB?2,BC?1,AA1?34．在长方体，则BC1与平面

BB1D1D所成的角?可用反三角函数值表示为??____________．

答案：O

O

5．若取地球的半径为6371米，球面上两点A位于东经12127'，北纬318'，B

OO

位于东经12127'，北纬255'，则A、B两点的球面距离为_____________千米

(结果精确到1千米)． 答案：673

2

6．已知圆锥的母线长为5cm，侧面积为15? cm，则此圆锥的体积为

__________cm．

答案：12?

7．若圆锥的底面半径和高都是2，则圆锥的侧面积是_____________．

答案：

8．如图，是一个无盖正方体盒子的表面展开图，A、B、C为其上的三个点，则

3

在正方体盒子中，?ABC?____________.

17高三立体几何专题练习(含答案)_立体几何练习题

?3

9．一个圆柱形容器的轴截面尺寸如右图所示，容器内有一个实心的球，球的直径恰等于圆柱的高.现用水将该容器注满，然后取出该球（假设球的密度大于水且操作过程中水量损失不计），则球取出后，容器中水面的高度为__________ cm. （精确到0.1cm）

答案：答案：8.3

10．如图，用铁皮制作一个无盖的圆锥形容器，已

知该圆锥的母线与底面所在平面的夹角为45?，容

器的高为10cm．制作该容器需要铁皮面积为

__________cm2．（衔接部分忽略不计，结果保留整数）

答案：444 cm2

11．如图，圆锥的侧面展开图恰好是一个半圆，则该圆锥的

母线与底面所成的角的大小是__________ . 答案：60

??

12．如图，?ABC中，?C?90，?A?30，BC?1．在三角形内挖去半圆

?

（圆心O在边AC上，半圆与BC、AB相切于点C、M，与AC交于N），则图 中阴影部分绕直线AC旋转一星期所得旋转体的体积为__________ ．

5?

答案：27

13．如图所示，以圆柱的下底面为底面，并以圆柱的上底面圆心为顶点作圆锥，

则该圆锥与圆柱等底等高。若圆锥的轴截面是一个正三角形，则圆柱的 侧积面与圆锥的侧面积之比为__________ 答案：2

14．一个圆锥形的空杯子上面放着一个球形的冰淇淋，圆锥底的直径与球的直径

相同均为10，如果冰淇淋融化后全部流在空杯子中，并且不会溢出杯子，则杯子的高度最小为____________． 答案：20

二、选择题（本大题满分20分，每小题5分） 15．如图，P为正方体

D1A1

P

DA

C1

ABCD?A1B1C1D1的中心，△PAC在该正方体各个面上

C1

的射影可能是（ ）

A. (1)、(2)、(3)、(4) B.(1)、(3) C.(1)、(4) D.(2)、(4)

答案：C

16．给出下列命题：(1)三点确定一个平面；(2)在空间中，过直线外一点只能作

(1)(2)

(4)

一条直线与该直线平行；(3)若平面?上有不共线的三点到平面?的距离相等，

则?//?；(4)若直线a、b、c满足a?b、a?c,则b//c.其中正确命题的个数是 ( )

A．0个 B．1个 C．2个 D．3个

答案：B

2

24cm17. 已知长方体的表面积是，过同一顶点的三条棱长之和是6cm，则它的对

角线长是（ ）

B. 4cm

C.

D.

答案：D

18．用一个平面去截正方体，所得截面不可能是 （ ）．

（B） 平面六边形； （B）菱形； （C）梯形； （D）直角三角形

答案：D

三、解答题（本大题满分74分）

19．（满分14分）本题共有2小题，第1小题满分7分，第2小题满分7分．

如图：三棱锥P?ABC中，PA?底面ABC，若底 面ABC是边长为2的正三角形，且PB与底面ABC

A

?

所成的角为3．若M是BC的中点，求： （1）三棱锥P?ABC的体积；

（2）异面直线PM与AC所成角的大小（结果用反三角函数值表示）． [解]（1）因为PA?底面ABC，PB与底面ABC所成的角为 所以 ?PBA?

?

3

?

3

………2分 因为AB?2，所以PB?23…………4分

113

VP?ABC?S?ABC?PA???4?23?2 ………………6分

334

（2）连接PM，取AB的中点，记为N，连接MN，则MN//AC 所以?PMN为异面直线PM与AC所成的角 ………………7分 计算可得：PN?，MN?1，PM? ………………9分

cos?PMN?

1?15?132?

………………11分 10

………………12分 10

异面直线PM与AC所成的角为20．（本题满分14分）本题共有2个小题，第1小题满分6分，第2小题满分8分． 如图，在四棱锥P?ABCD中，底面ABCD是

边长为2的菱形，?ABC?60，PA?平面ABCD，

PC与平面ABCD所成角的大小为arctan2，M为 PA的中点．

C

D

（1）求四棱锥P?ABCD的体积；

（2）求异面直线BM与PC所成角的大小（结果用 反三角函数表示）． 答案：解：（1）连结AC，因为PA?平面ABCD， 所以?PCA为PC与平面ABCD所成的角……（2分）

PA

?2，而AC?2， 由已知，tan?PCA?AC

所以PA?4．……（3分）

底面积S?2?2?sin60?2，……（4分） 所以，四棱锥P?ABCD的体积

118．……（6分） V?Sh??2?4?

333

（2）连结BD，交AC于点O，连结MO，

因为M、O分别为PA、AC的中点，所以MO∥PC，

所以?BMO（或其补角）为异面直线BM与PC所成的角．……（8分） 在△BMO中，BO?3，BM?22，MO?，……（10分） （以下由余弦定理，或说明△BMO是直角三角形求得）

6或或．……（13分） 445

所以，异面直线BM与PC所成角的大小为arcsin（或另外两个答案）．……（14分.

4?BMO?arcsin

21. （本题满分14分）第1小题8分，第2小题6分.

如图，正四棱锥P?ABCD底面的四个顶点A,B,C,D在球O 的同一个大圆上，点P在球面上，且已知

VP?ABCD?

163.

P

(1)求球O的表面积；

BCPCMAM(2)设为中点，求异面直线与所成角的大小

答案：解：(1)S?16?； (2)arccos

10

22．（本题满分16分，第1小题7分，第2小题9分）

如图，在直三棱柱ABC?A1B1C1中，

C1

A1

B1

CC1?

A?C

B2?，C?ACB?90?.

（1） 下图给出了该直三棱柱三视图中的主视图，请据此画出它的左视图和俯视图；

（2） A

C

B

第22题图

若P

是AA1的中点，求四棱锥

B1?C1A1PC的体积.

答案：

?

?2??2

?

23．（本题满分16分，第1小题8分，第2小题8分）

如图，在直三棱柱ABC?A1B1C1中，CC1?AC?BC，

?ACB?90?，P是AA1的中点，Q是AB的中点.

A1

C1B1

P

B

A

17高三立体几何专题练习(含答案)_立体几何练习题

（1）求异面直线PQ与B1C所成角的大小；

1

（2）若直三棱柱ABC?A1B1C1的体积为2，求四棱锥C?BAPB1的体积. 解：（1）如图，建立空间直角坐标系.不妨设CC1?AC?BC?2.

依题意，可得点的坐标P?2,0,1?，Q?1,1,0?，B1?0,2,2?.

???????? 于是，PQ???1,1,?1?，B1C??0,?2,?2?.

???????? 由PQ?B1C?0，则异面直线PQ与B1C所成角的大小为?. 2

（2）解：连结CQ. 由AC?BC，Q是AB的中点，得CQ?AB; 由AA1?面ABC，

CQ面ABC，得CQ?AA1.

又AA1?AB?A，因此CQ?面ABB1A1 由直三棱柱ABC?A1B1C1的体积为

所以，四棱锥C?BAPB1的体积为

1. ?CC1?AC?BC?1.

可得CQ?22

11?1?1?1VC?BAPB1??CQ?SBAPB1????1??. 33?2?2?4

二 : 几何体的外接球专练

几何体的外接球专练

1 ．（2012课标）平面α截球O的球面所得圆的半径为1,球心O到平面α2,则此球的体积为（ ） 2. 一个六棱柱的底面是正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为9，底面周长为３，则这个球的体积为 .

8

3. 已知各顶点都在同一个球面上的正四棱柱的高为4，体积为16，则这个球的表面积是 . 4. 正四棱锥S?

ABCD的底面边长和各侧棱长都为为 .

5.（09全国）直三棱柱ABC-A1B1C1中AB=AC=AA1=2，?BAC?1200，则其外接球的表面积： 若?BAC?600则其外接球的表面积：若?BAC?900则其外接球的表面积：6. （2012辽宁理）已知正三棱锥P?ABC,点P,A,B,C

互相垂直,则球心到截面ABC

的距离为________.

,若

S、A、B、C、D都在同一球面上，则此球的体积

PA,PB,PC两两

D

CB

7.（安徽）表面积为??√??的正八面体的外接球的体积：

。 8. 在矩形ABCD中，AB?4,BC?3，沿AC将矩形ABCD折成一个直二面角B

?AC?D，则四面体ABCD的

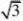
图4

外接球的体积为A.125?

B.125? C.125? D.125?

12963

9. 一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的外接球的

表面积为 （ ）

16?A．3

8?B．3

C．．

10.一个四面体中，如果有三条棱两两互相垂直且满足垂足不是同一点，这三条棱就象中国武术中的兵器---三

节棍 我们常把这类四面体称为“三节棍体”。若某“三节棍体”的四顶点在空间直角坐标系中的坐标分别是：（0，0，0），（0，2，0），（2，2，0），（2，2，2）则此“三节棍体”的外接球的表面积： . 11. 在三棱柱ABC-A1B1C1中，已知AA??平面ABC，AA??2，BC?2 则此三棱柱的外接球的体积： 。

12.棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图，则图中三角形(正四面体的截面)的面积是 .

，?BAC?

?

2

13．（2012新课标）已知三棱锥S?ABC的所有顶点都在球O的求面上,?ABC是边长为1的正三角形径,且SC?2;则此棱锥的体积为 （ ）A．

6

B．

6

C．

3

D．

2

.若

14．（2012辽宁）已知点P,A,B,C,D是球O表面上的点,PA⊥平面ABCD,四边形ABCD是边长为PA=2

,则△OAB的面积为______________.

三 : 立体几何练习题及答案75

数学立体几何练习题

一、选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个是符合题目要求的．

1．如图，在正方体ABCD－A1B1C1D1中，棱长为a，M、N分别为A1B和AC上

的点，A1M＝AN＝

a

，则MN与平面BB1C1C的位置关系是( ) 3

A．相交 B．平行 C．垂直 D．不能确定

2．将正方形ABCD沿对角线BD折起，使平面ABD⊥平面CBD，E是CD中点，则?AED的大小为（ ）

A.45? B.30? C.60? D.90?

3．PA，PB，PC是从P引出的三条射线，每两条的夹角都是60o，则直线PC与平面PAB

所成的角的余弦值为（ ）

A．

12

B

。

2

C

3

D

3

4．正方体ABCD—A1B1C1D1中，E、F分别是AA1与CC1的中点，则直线ED与D1F所成角的余弦值是

A．

15

13

12

2

B。 C。 D

5． 在棱长为2的正方体ABCD?A1B1C1D1中，O是底面ABCD的中心，E、F分别是CC1、

AD的中点，那么异面直线OE和FD1所成的角的余弦值等于（ ）

A．

5

B．

23

C．

55

D．

5

）

6．在正三棱柱ABC-A1B1C1中，若AB=2，A A1=1，则点A到平面A1BC的距离为（

A．

34

B．

32

C．

334

D．3

7．在正三棱柱ABC-A1B1C1中，若AB=1,则AB1与C1B所成的角的大小为 （ ）

A.60oB. 90oC.105oD. 75o

8．设E，F是正方体AC1的棱AB和D1C1的中点，在正方体的12条面对角线中，与截面

A1ECF成60°角的对角线的数目是（ ）

A．0 B．2 C．4 D．6 二、填空题：本大题共6小题，每小题5分，共30分．

9.在正方体ABCD－A1B1C1D1中，M、N分别为棱AA1和BB1的中点，则

?????????

sin〈CM，D1N〉的值为_________.

10．如图，正方体的棱长为1，C、D分别是两条棱的中点， A、B、M是顶点，

那么点M到截面ABCD的距离是 .

C

M B

11．正四棱锥P-ABCD的所有棱长都相等，E为PC中点，则直线AC与截面BDE所成的角为 ．

12．已知正三棱柱ABC-A1B1C1的所有棱长都相等，D是A1C1的中点，则直线AD与平面

B1DC所成角的正弦值为. 13

．已知边长为的正三角形ABC中，E、F分别为BC和AC的中点，PA⊥面ABC，

且PA=2，设平面?过PF且与AE平行，则AE与平面?间的距离为 ． 14．棱长都为2的直平行六面体ABCD—A1B1C1D1中，∠BAD=60°，则对角线A1C与侧面DCC1D1所成角的余弦值为________.

三、解答题:本大题共6小题，共80分。解答需写出必要的文字说明、推理过程或计算步骤.

15．如图，直三棱柱ABC

?A1B1C1，底面?ABC

中，CA＝CB＝1，?BCA

?90

?

，棱AA1

?2

，M、

N分别A1B1、A1A是的中点． (1) 求BM的长； (2) 求cos?BA1,CB1?的值； (3) 求证：A1B?C1N．

y

16．如图，三棱锥P—ABC中， PC?平面ABC，PC=AC=2，AB=BC，x D是PB上一点， 且CD?平面PAB．

(1) 求证：AB?平面PCB； P (2) 求异面直线AP与BC所成角的大小； (3)求二面角C-PA-B的大小的余弦值．

C

17．如图所示，已知在矩形ABCD中，AB=1，BC=a（a>0），PA⊥平面AC，且PA=1．

P （1）试建立适当的坐标系，并写出点P、B、D的坐标； （2）问当实数a在什么范围时，BC边上能存在点Q，

使得PQ⊥QD？

（3）当BC边上有且仅有一个点Q使得PQ⊥QD时， 求二面角Q-PD-A的余弦值大小．

18. 如图，在底面是棱形的四棱锥P?ABCD中，?ABC

A

Q

D

C

?60,PA?AC?a,PB?PD?

?

2a

，点E

在PD上，且PE:ED＝2:1．

(1) 证明 PA?平面ABCD；

(2) 求以AC为棱，EAC与DAC为面的二面角?的大小；

(3) 在棱PC上是否存在一点F，使BF∥平面AEC？证明你的结论．

19. 如图四棱锥P—ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上，且PG＝4，AG?

20.已知四棱锥S－ABCD的底面ABCD是正方形，SA⊥底面

ABCD，E是SC上的任意一点． (1)求证：平面EBD⊥平面SAC；

(2)设SA＝4，AB＝2，求点A到平面SBD的距离； SA

(3)的值为多少时，二面角B－SC－D的大小为120°？

AB

理科立体几何训练题（B）答案

一、选择题

二、 9.

填空题

E

C D

13

GD，BG⊥GC，GB＝GC＝2，E是BC的中点．

C

(1)求异面直线GE与PC所成的角的余弦值； (2)求点D到平面PBG的距离；

(3)若F点是棱PC上一点，且DF⊥GC，求

PFFC

的值．

3452234

10． ° 12． 13． 14 93543

三、解答题

15解析：以C为原点建立空间直角坐标系O?xyz. (1) 依题意得B（0，1，0），M（1，0，1）．?

(1?0)?(0?1)?(1?0)

2

2

2

?3

.

y

(2) 依题意得A1（1，0，2），B（0，1，0），C（0，0，0），B1（0，

1，2）

.

?BA

1?(1,?1,2),CB1?(0,1,2),BA1?CB1?3?

6?

5

?cos?BA1,CB1??

?

3010

.

(3) 证明：依题意得C1（0，0，2），N(

?A1B?C1N??

12?12

?0?0,?A1B?C1N

1111

,,2),?A1B?(?1,1,?2),C1N?(,,0)2222

.

16．解析： (1) ∵PC⊥平面ABC,AB?平面ABC， ∴PC?AB.∵CD?平面PAB，AB?平面PAB， ∴CD?AB．又PC?CD?C，∴AB?平面PCB． (2 由(I) AB?平面PCB，∵PC=AC=2，

又∵AB=BC，可求得BC=．以B为原点， 如图建立坐标系．则Ａ（０,2,０），Ｂ（0,0,0），C（０,0），P（０,2）．

????????

=(2,－，=(． BCAP?????

则AP?BC=．

????????

????????2AP?BCcos?AP,BC?==

AP?BC22?

P

z

= 2

12

．

∴异面直线AP与BC所成的角为

?

3

．

????????

（3）设平面PAB的法向量为m= (x，y，z)．AB=(0, AP=(

－2,2)，

x

y

????????y?0,?AB?m?0,??0,则????

即解得?令z= -1,得 m= (?

x??????2z?0.?AP?m?0.

2，0，-1)．

?

由PC?平面ABC易知：平面PAC?平面ABC，取AC的中点E，连接BE，则BE为

?

平面PAC的一个法向量，BE?(为n= (1，1，0)．

cos?m,n??

m?nmn

223

,

22

,0)?

22

(1,1,0)，故平面PAC的法向量也可取

=

23?

2

?

3

. ∴二面角C-PA-B的大小的余弦值为

33

．

17．解析：（1）以A为坐标原点，AB、AD、

别为x、y、z轴建立坐标系如图所示． ∵PA=AB=1，BC=a，

∴P（0，0，1），B（1，0，0），

D（0，a，0）．

（2）设点Q（1，x，0），则

????????

DQ?(1,x?a,0),QP?(?1,?x,1)．

由DQ?QP?0，得x2-ax+1=0．

显然当该方程有非负实数解时，BC边上才存在点Q，使得PQ⊥QD，故只须⊿=a2-4≥0． 因a>0，故a的取值范围为a≥2．

（3）易见，当a=2时，BC上仅有一点满足题意，此时x=1，即Q为BC的中点．

取AD的中点M，过M作MN⊥PD，垂足为N，连结QM、QN．则M（0，1，0），P（0，0，1），D（0，2，0）．∵D、N、P三点共线，

??????????????MD??MP(0,1,0)??(0,?1,1)(0,1??,?)∴MN?． ??

1??1??1??

?????????????

又PD?(0,2,?1)，且MN?PD?0，

????????

故

(0,1??,?)1??

?(0,2,?1)?

2?3?1??

?0???

23

．

?????

于是MN?

(0,1?1?

22,)

?(0,1,2)

．

255

3

???????????????????????12

故NQ?NM?MQ??MN?AB?(1,?,?)．

55

????????

12

∵PD?NQ?0?2?(?)?(?1)?(?)?0，

55

∴PD?NQ．（资料来源：www.maths168.com） ∴∠MNQ为所求二面角的平面角．

?????????NM?NQ∵cos?MNQ??，

6|NM|?|NQ|

????????

注：该题还有很多方法解决各个小问，以上方法并非最简.

18解析：（1）传统方法易得证明（略）

（2）传统方法或向量法均易解得??30?；

（3）解 以A为坐标原点，直线AD,AP分别为y轴、z轴，过A点垂直于平面PAD的直线为x轴，建立空间直角坐标系（如图）．由题设条件，相关各点的坐标为

A(0,0,0),B(

32a,?

12a,0),C(

23

13

32

a)

a,

12

a,0)

D(0,a,0),P(0,0,a),E(0,a,

32a,12a,0)

所以

AE?(0,

23

a,

13

a)，AC?(，

B

立体几何练习题及答案75_立体几何练习题

AP?(0,0,a),PC?(

32

12

32

a,

12

a,?a)

??PC?(

32

BP?(?a,a,a)

，设点F是棱PC上的点，PF

?a,

12

?a,??a)

，其中0??

?1

，则

?3a(1??)?a?1?

22?

3112?1

BF?BP?PF?(a(??1),a(1??),a(1??))．令BF??1AC??2AE得?a(1??)?a?1?a?2

2223?2

1?a(1??)?a?2

?3?

解得?

?

12

,?1??

12

,?2?

32

，即?

?

12

BF

??

12

AC?

32

AE

BF,AC,AE．亦即，F是PC的中点时，

共面，又BF

?

平面AEC，所以当F是PC的中点时，BF∥平面AEC．

19解析：(1)以G点为原点，GB、GC、GP为x轴、y轴、 z轴建立空间直角坐标系，则B(2，0，0)，C(0，2，0)，

P(0，0，4)，故E(1，1，0)，GE＝(1，1，0)， PC＝(0，2，4)。

22?

20

10

cos?GE，PC???

，

D

∴GE与PC所成的余弦值为

10

．

E

C

(2)平面PBG的单位法向量n＝(0，±1，0) ∵GD?

34AD?

34

BC?(?

3232

，0)，

32

∴点D到平面PBG的距离为|GD?n |＝.

3

333

，0)?(，y?，z)。 2222

(3)设F(0，y，z)，则DF?(0，y，z)?(?

∵DF?GC，∴DF?GC?0，（资料来源：www.maths168.com） 即(，y?

23

32

，z)?(0，2，0)?2y?3?0，

32

∴y?

32

, 又PF??PC，即(0，，z－4)＝λ(0，2，－4)， ∴z=1，

故F(0，

32

?3)，FC?(0，?1)，∴，1) ，PF?(0，

2

2

31

PFPF

PCFC

?

2

?3。

20解析：(1)∵SA⊥平面ABCD，BD?平面ABCD，∴SA⊥BD，

∵四边形ABCD是正方形，∴AC⊥BD，∴BD⊥ 平面SAC， ∵BD?平面EBD，∴平面EBD⊥平面SAC.

(2)设AC∩BD＝F，连结SF，则SF⊥BD， ∵AB＝2，SA＝4，∴BD＝， SF＝＋AF＝4＋(2)＝3， 11

∴S△SBD·SF·2＝6，

22设点A到平面SBD的距离为h，

1114

∵SA⊥平面ABCD，∴·S△SBD·h＝·S△ABD·SA，∴6·h2·2·4，∴h

33234

即点A到平面SBD.

3

(3)设SA＝a，以A为原点，AB、AD、AS所在直线分别为x、y、z轴建立空间直角坐标系，为计算方便，不妨设AB＝1，则C(1,1,0)，S(0,0，a)，B(1,0,0)，D(0,1,0)，

????????????

∴SC＝(1,1，－a)，SB＝(1,0，－a)，SD＝(0,1，－a)，

再设平面SBC、平面SCD的法向量分别为n1＝(x1，y1，z1)，n2＝(x2，y2，z2)，

??????n1SC?x1?y1?az1?0则???? ???n1SB?x1?az1?0∴y1＝0，从而可取x1＝a，则z1＝1，∴n1＝(a,0,1)， ??????n2SC?x2?y2?az2?0

?????

??n2SB?x2?az2?0

∴x2＝0，从而可取y2＝a，则z2＝1，∴n2＝(0，a,1)， 1∴cos〈n1，n2〉＝

a＋1

11

要使二面角B－SC－D的大小为120°，则，从而a＝1，

a＋12即当

SAa

1时，二面角B

－SC－D的大小为120°. AB1

2

2

本文标题：立体几何练习题-17高三立体几何专题练习(含答案)
本文地址： http://www.61k.com/1135511.html