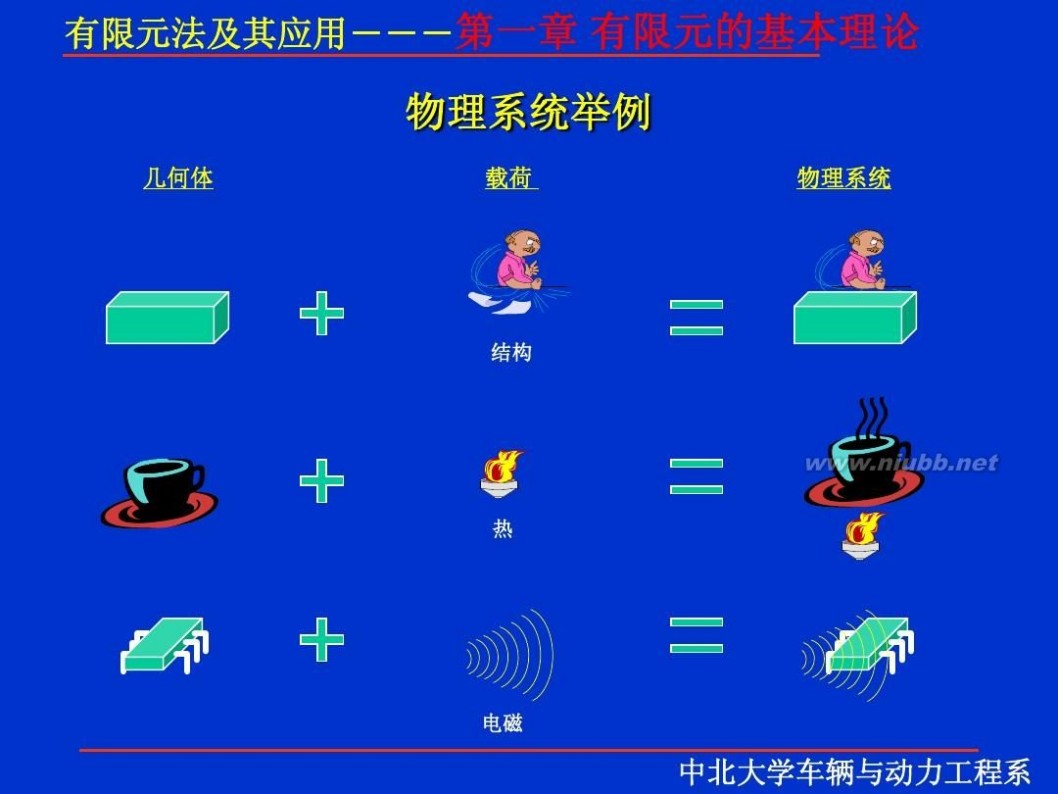
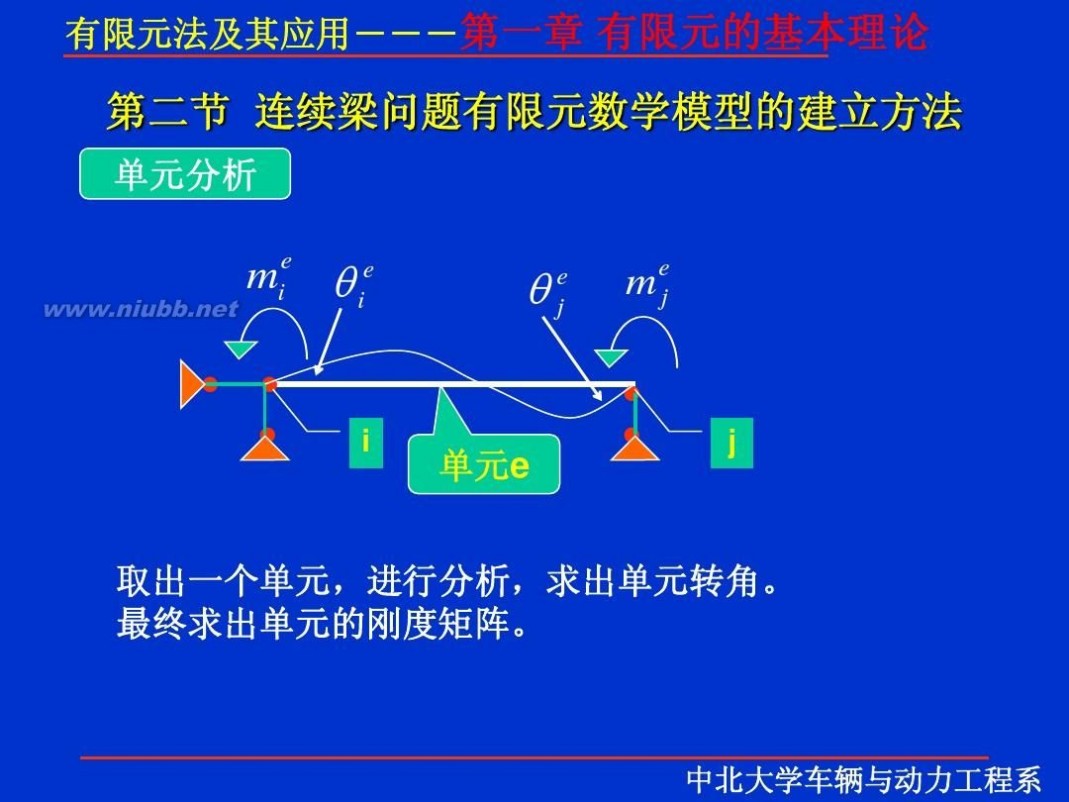
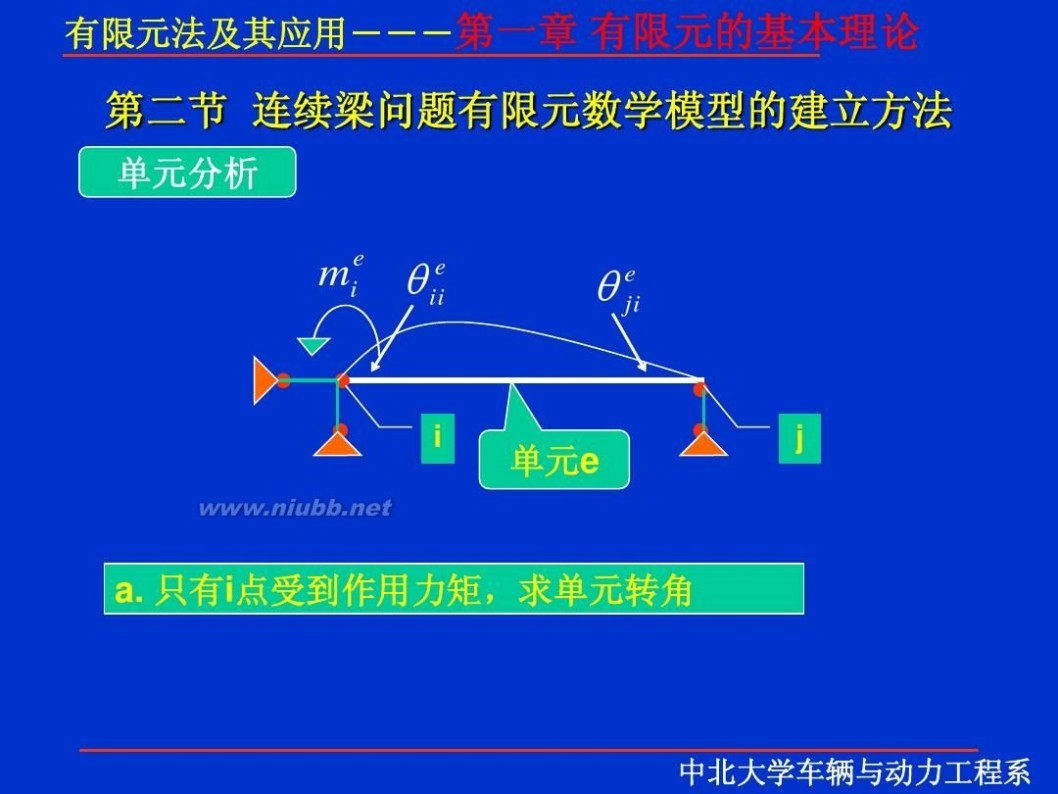
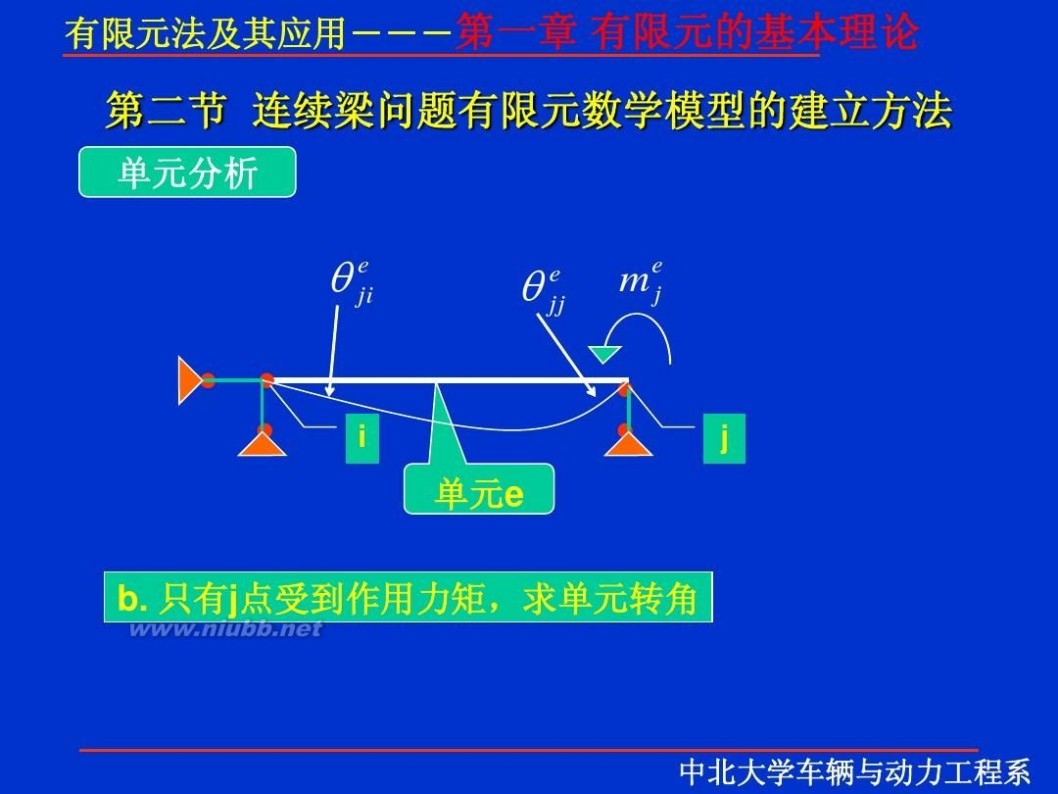
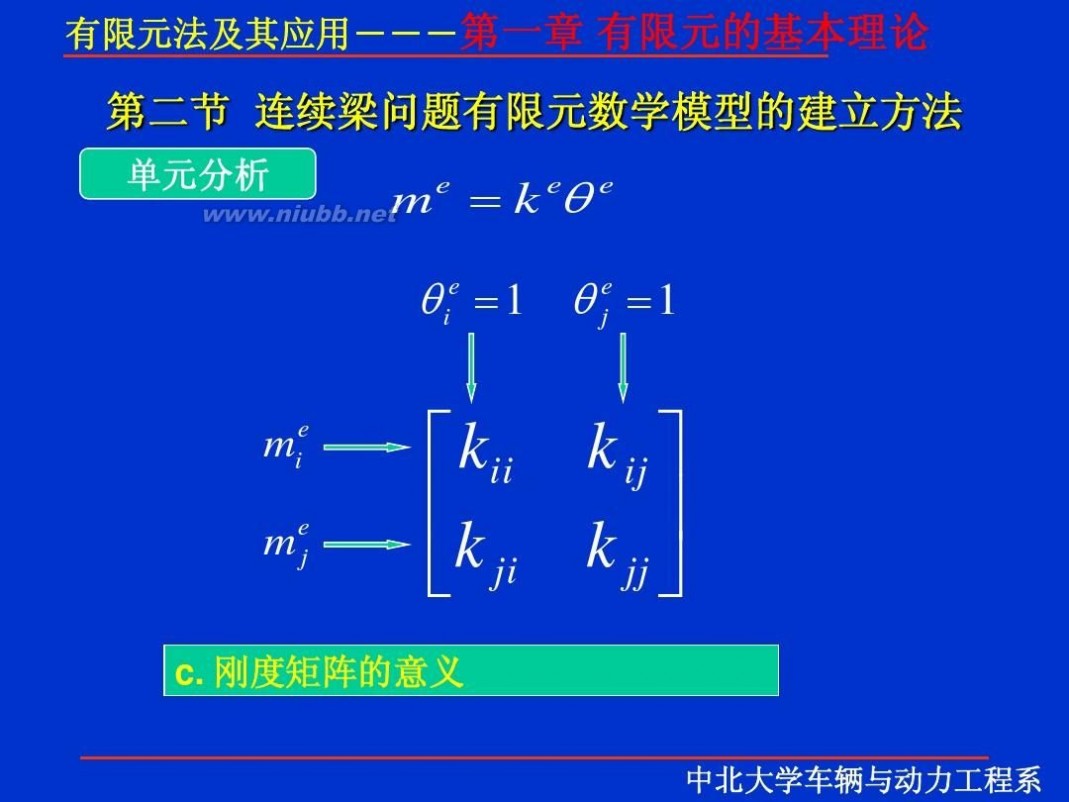
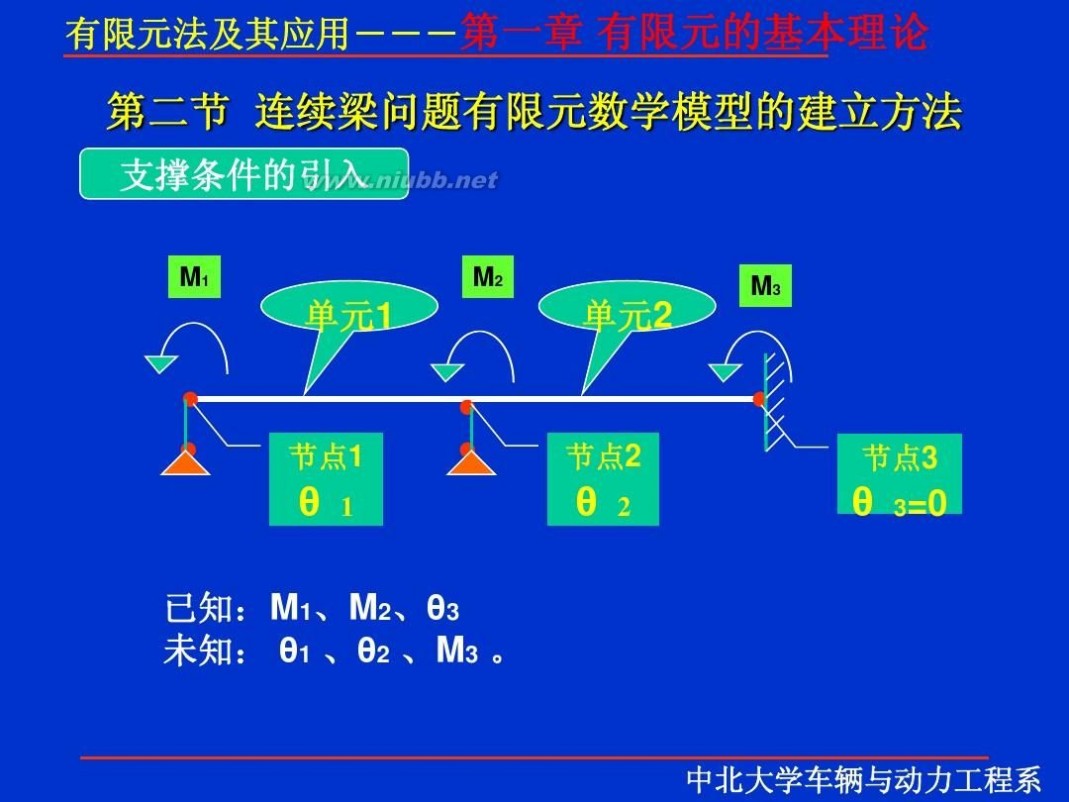
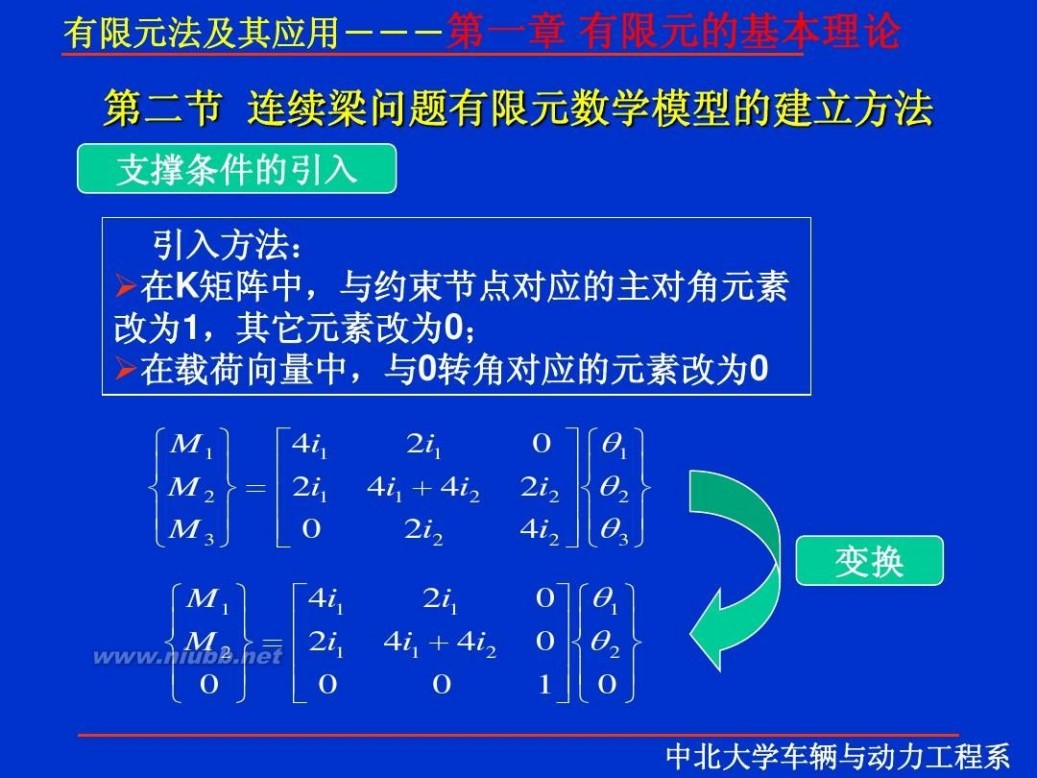
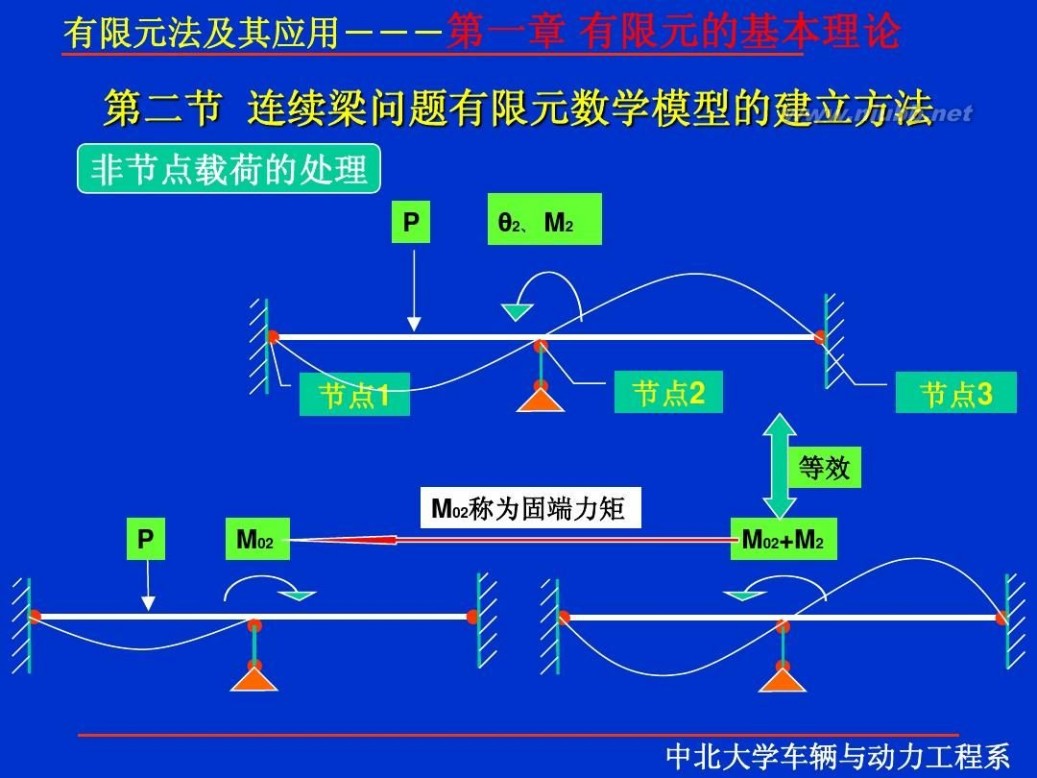
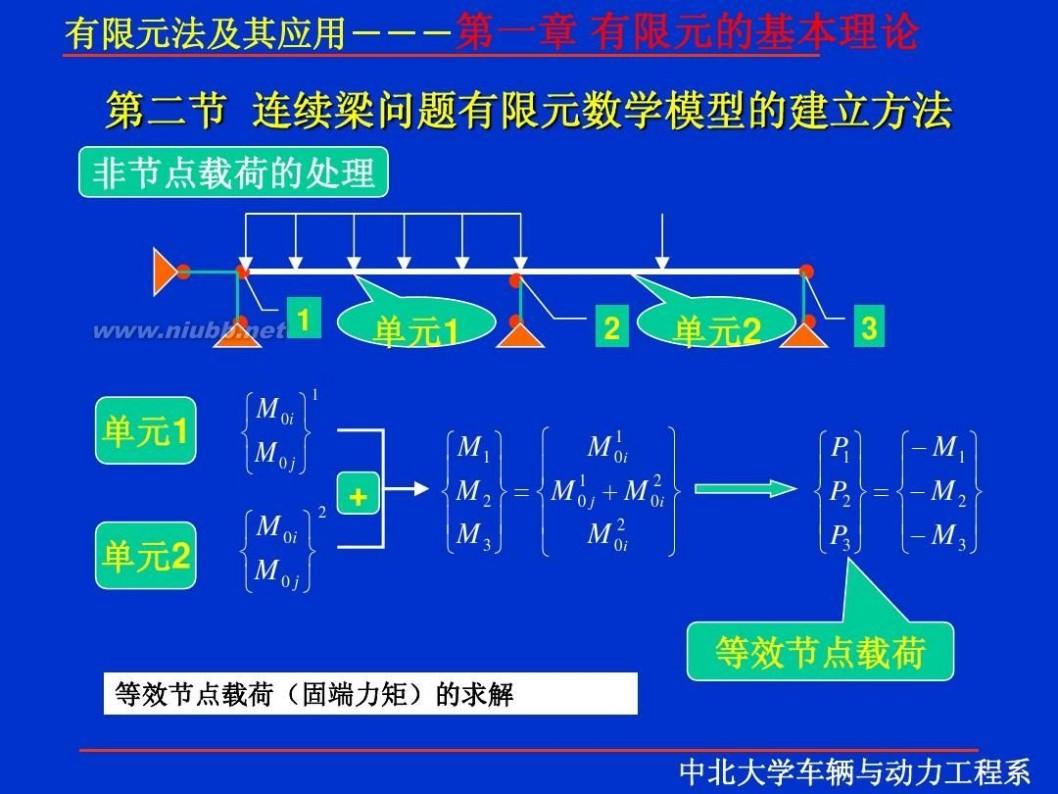
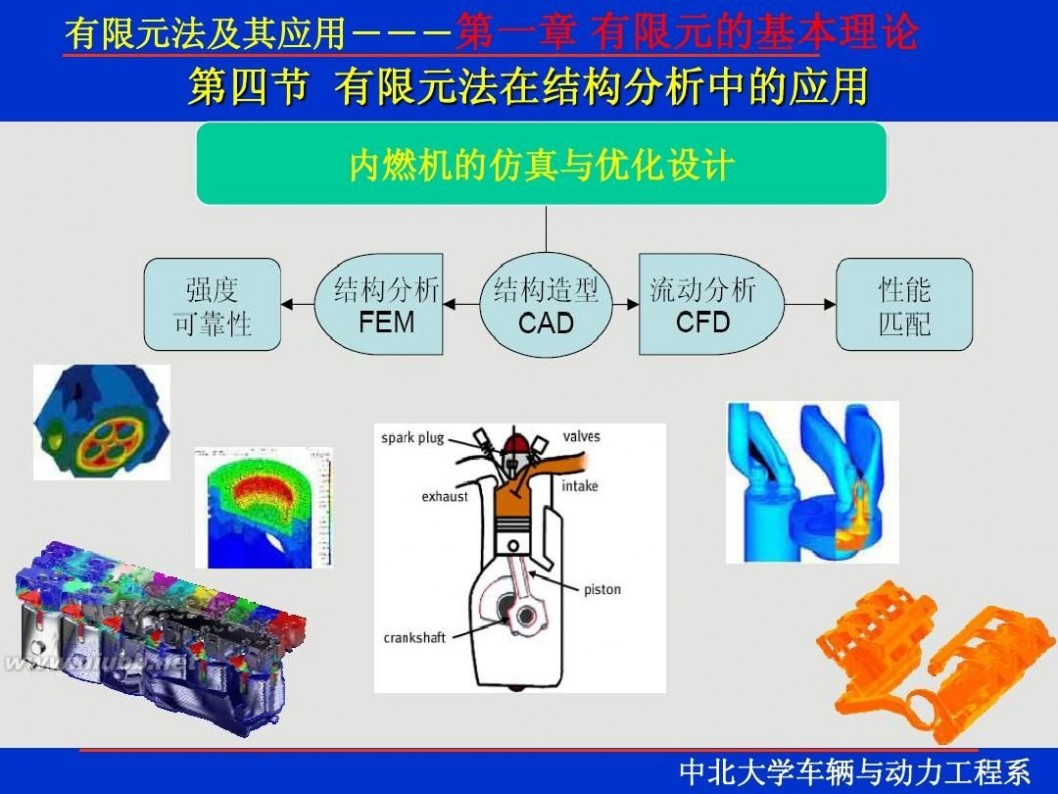
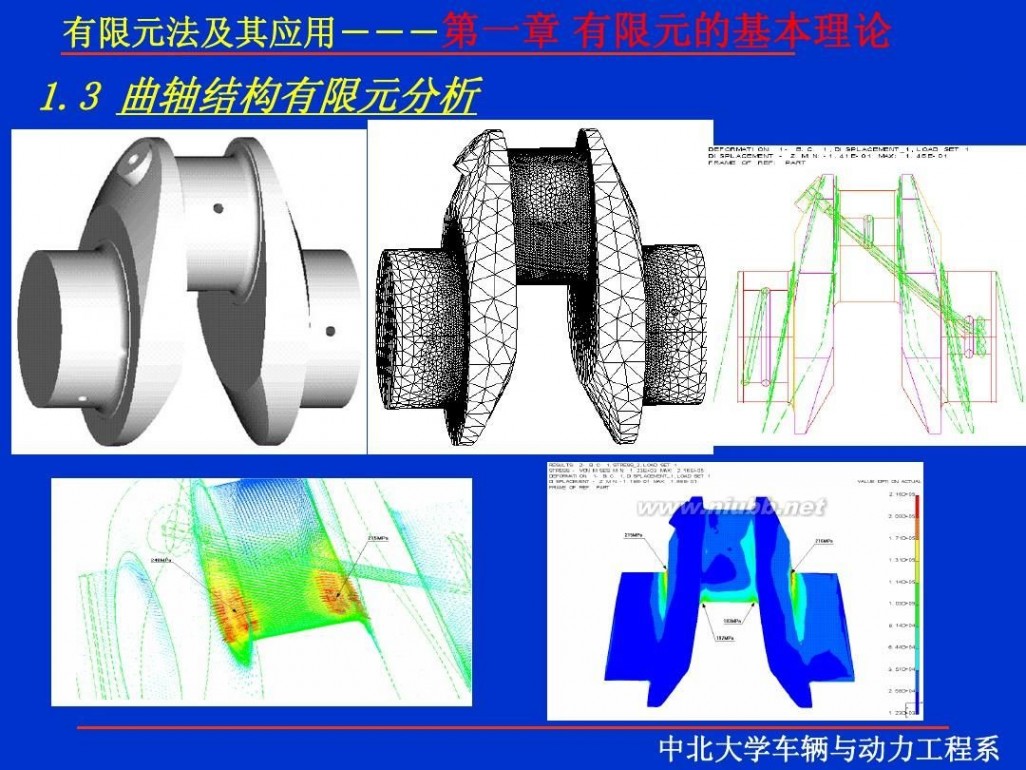
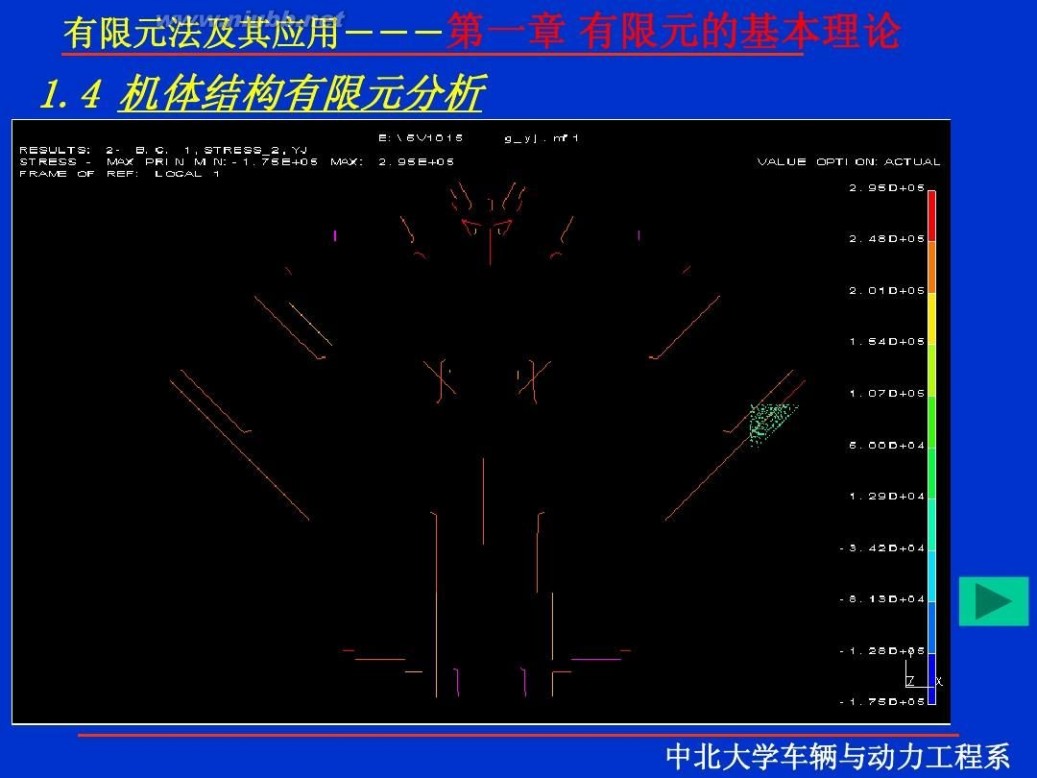
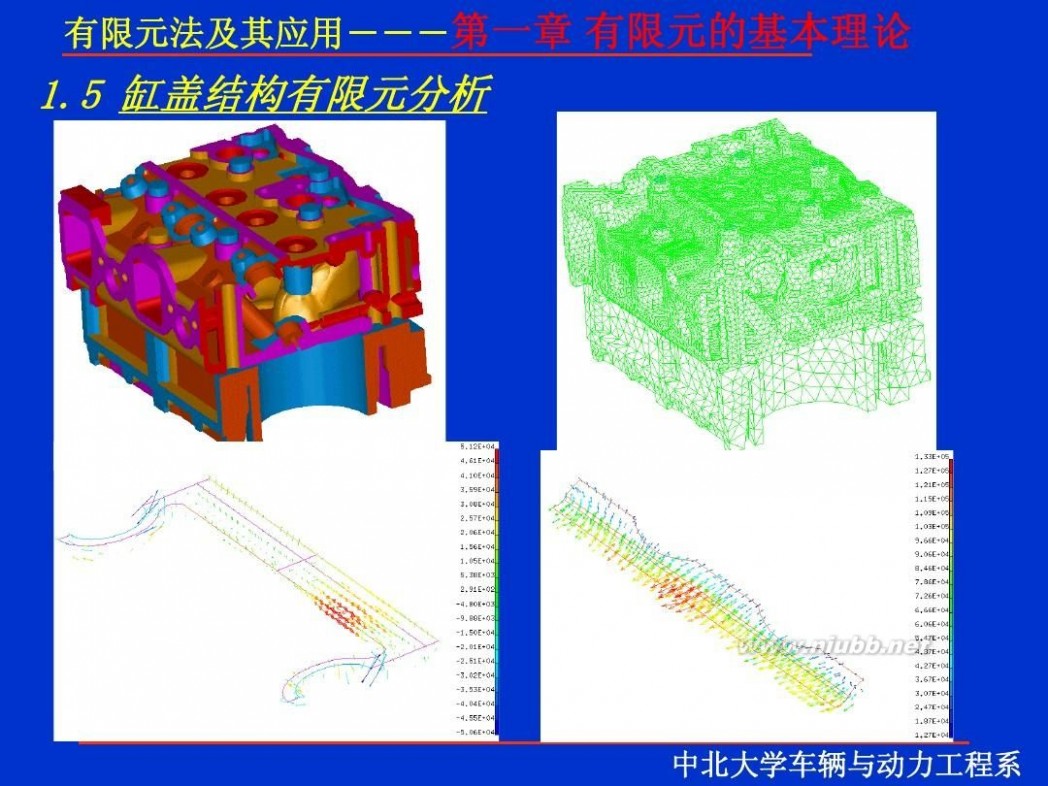
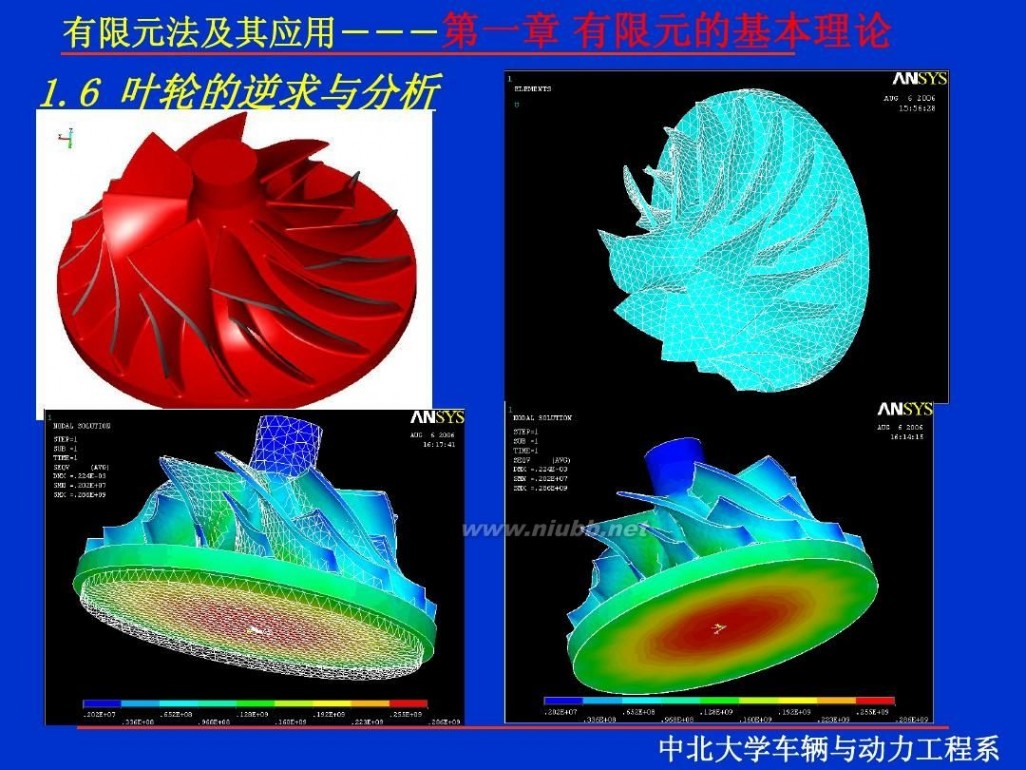
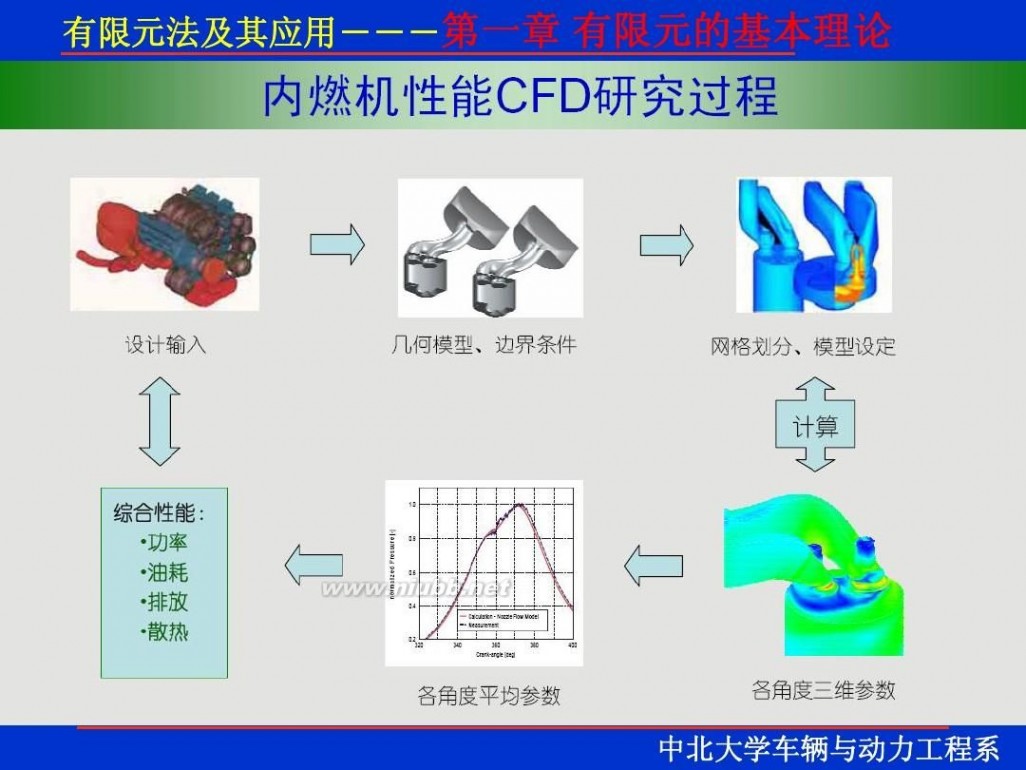
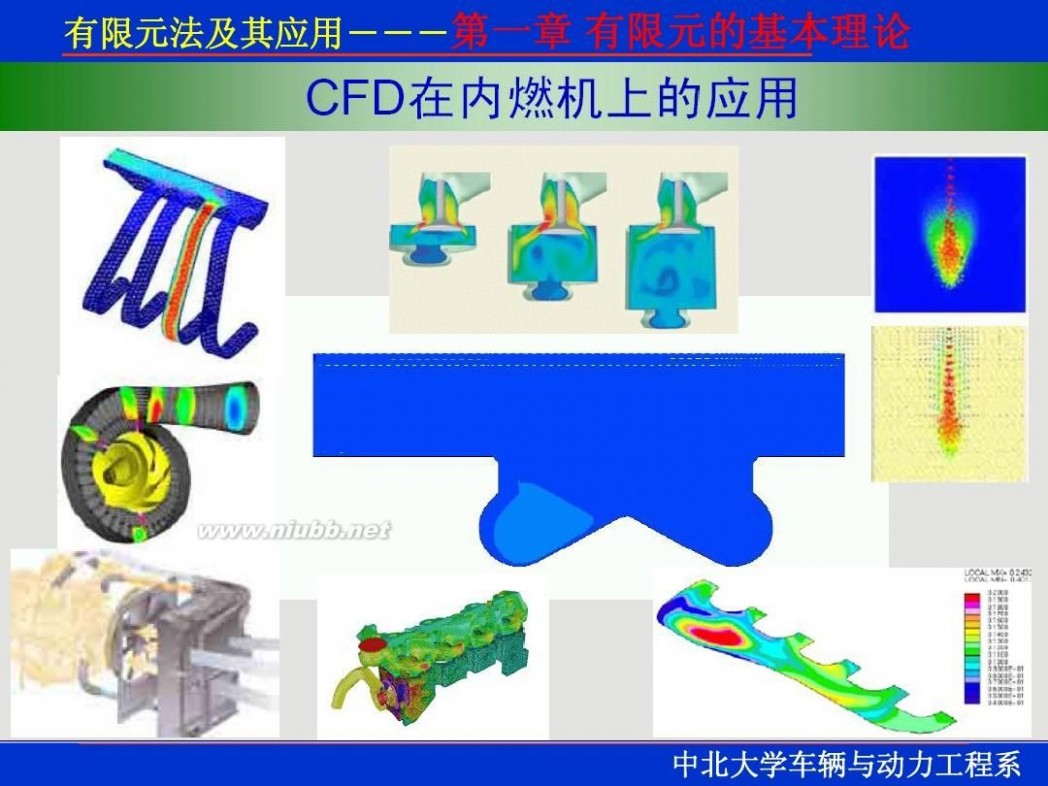
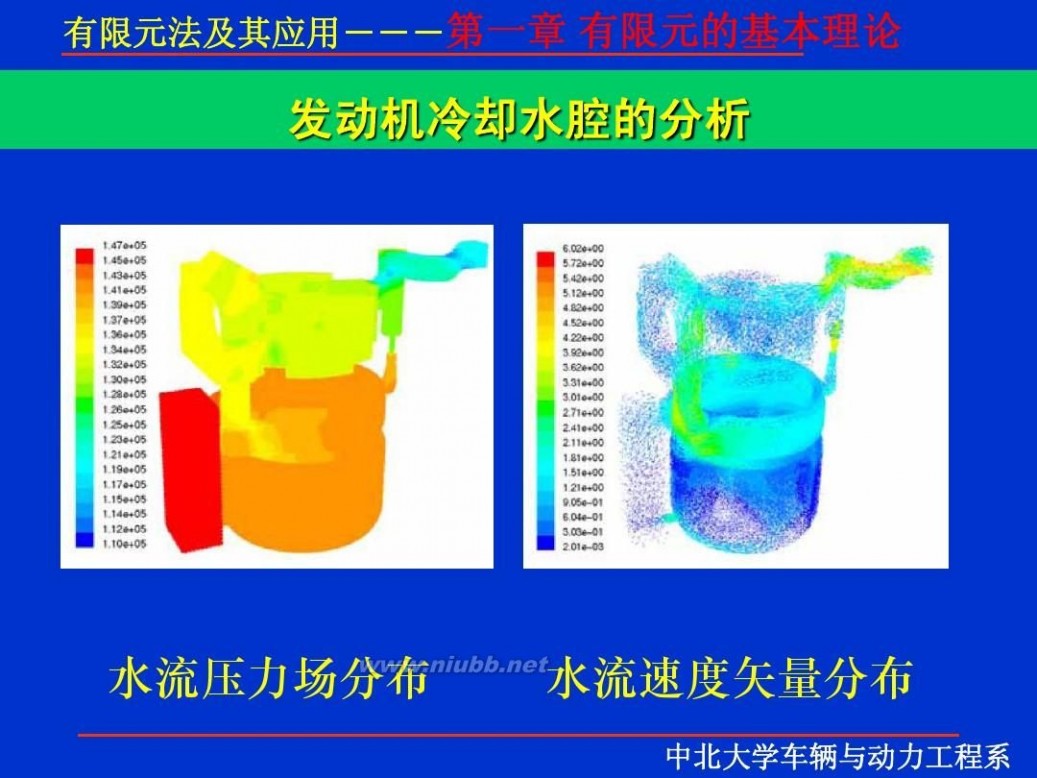
一 : 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
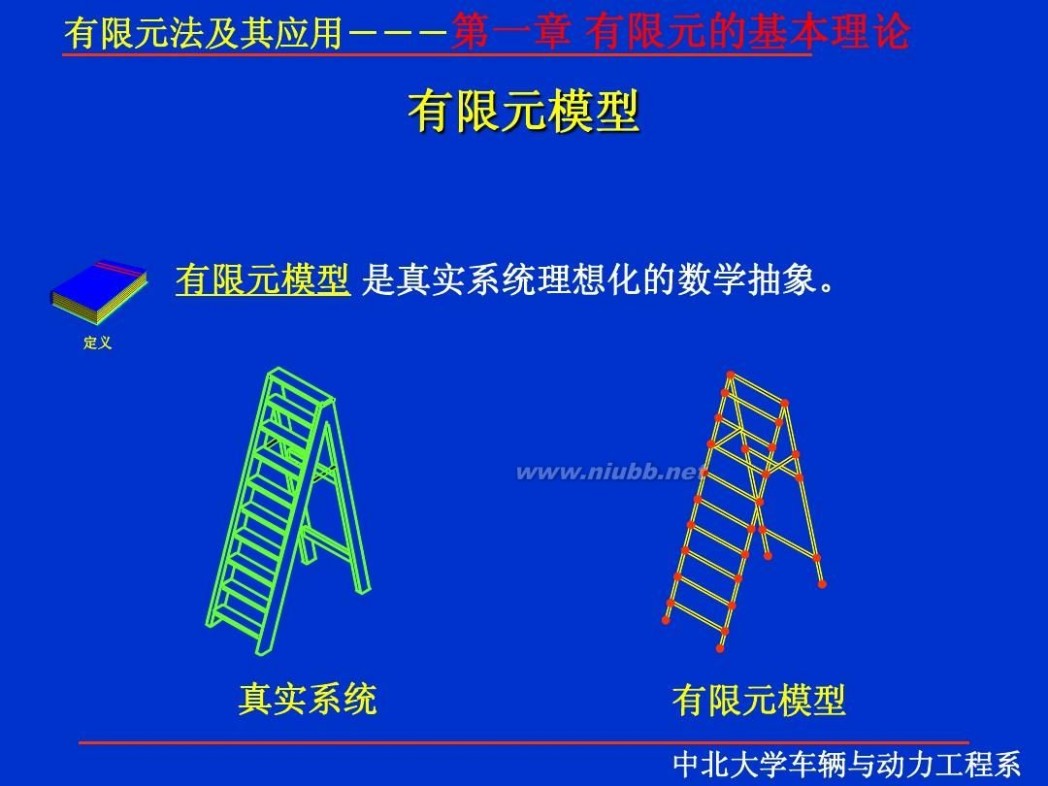
有限元 有限元理论
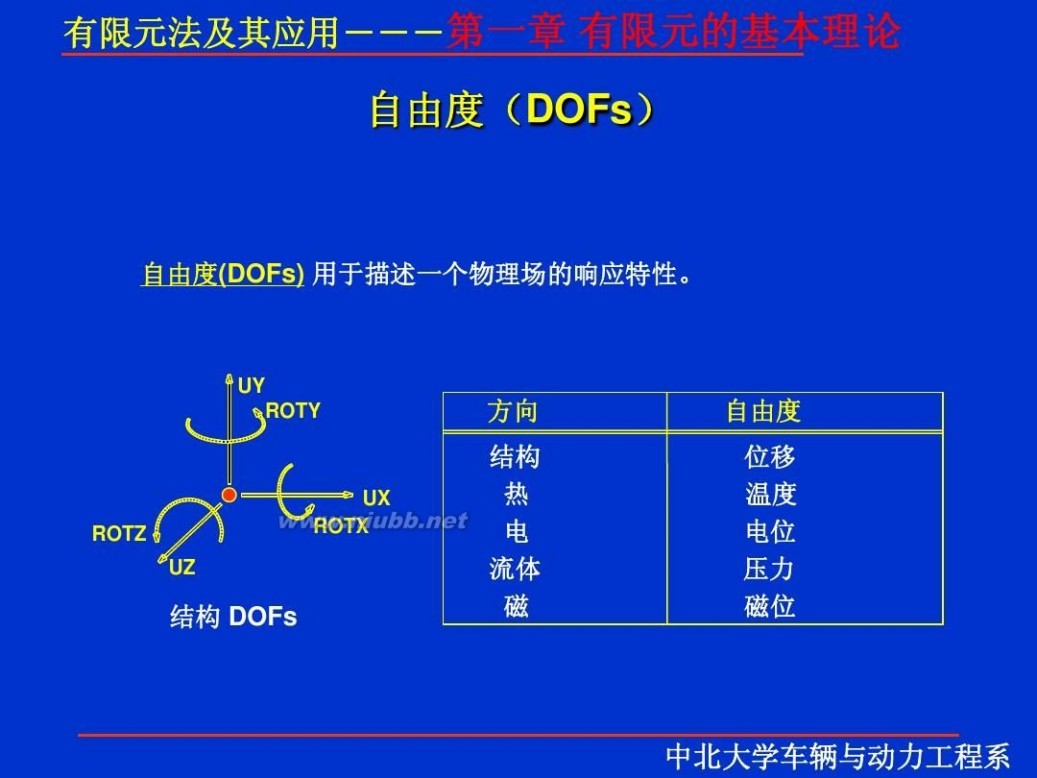
有限元 有限元理论
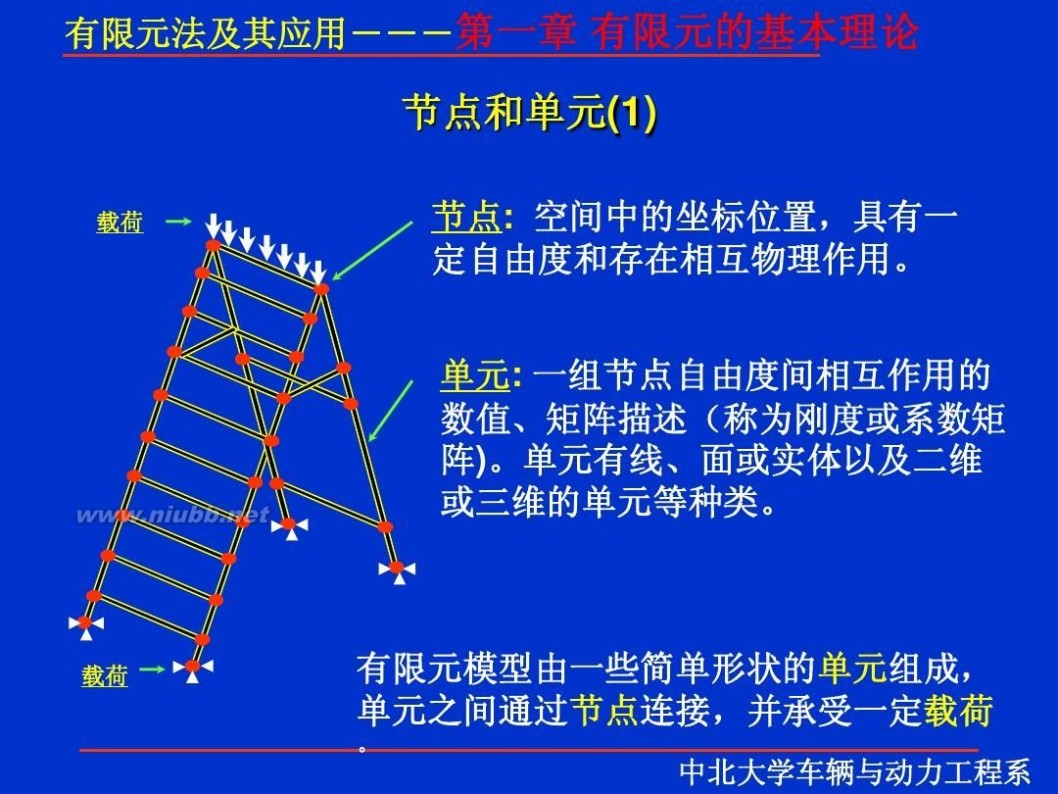
有限元 有限元理论
有限元 有限元理论

有限元 有限元理论
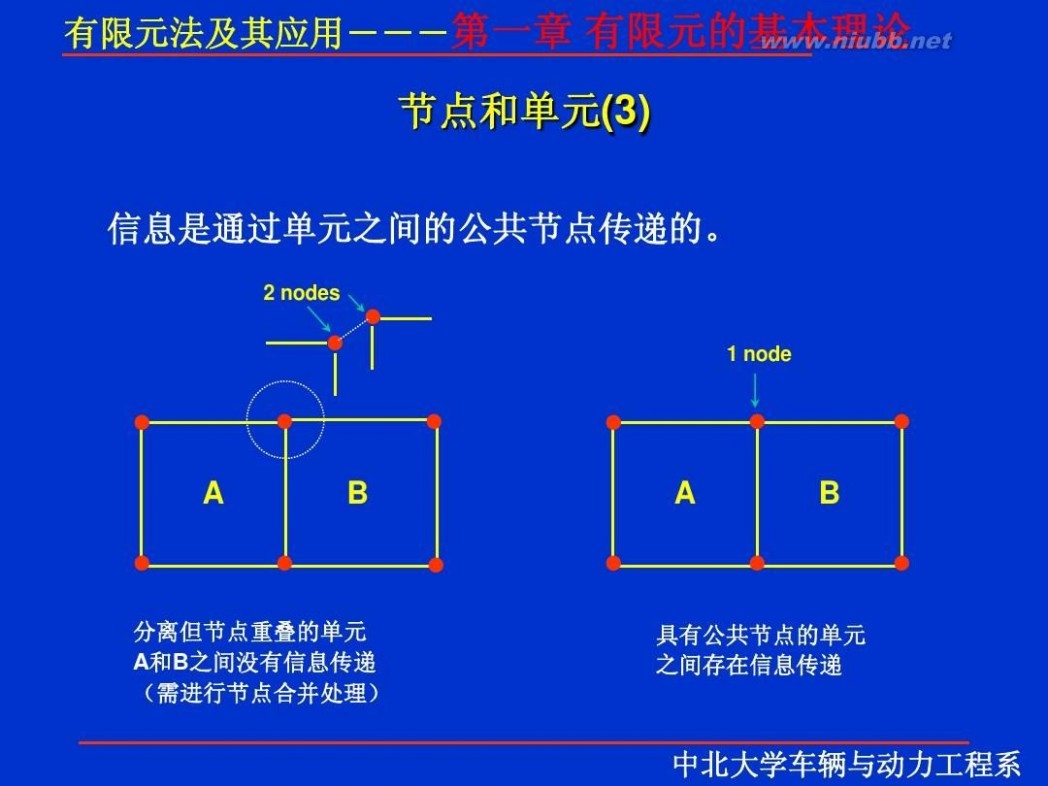
有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
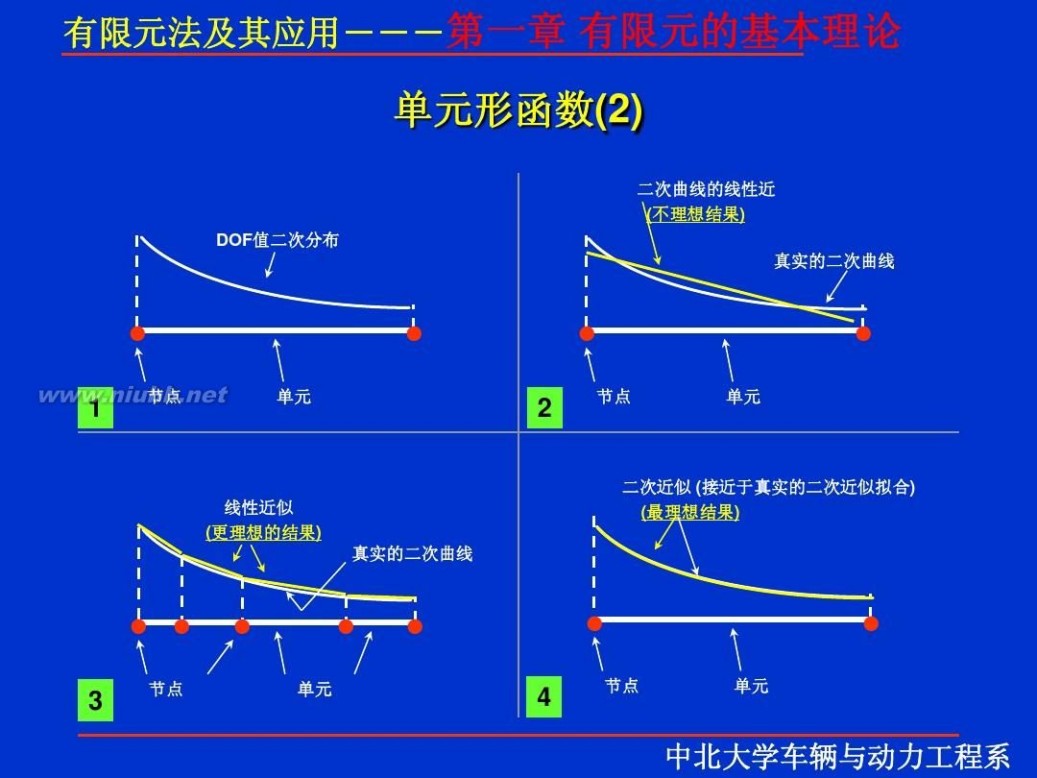
有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
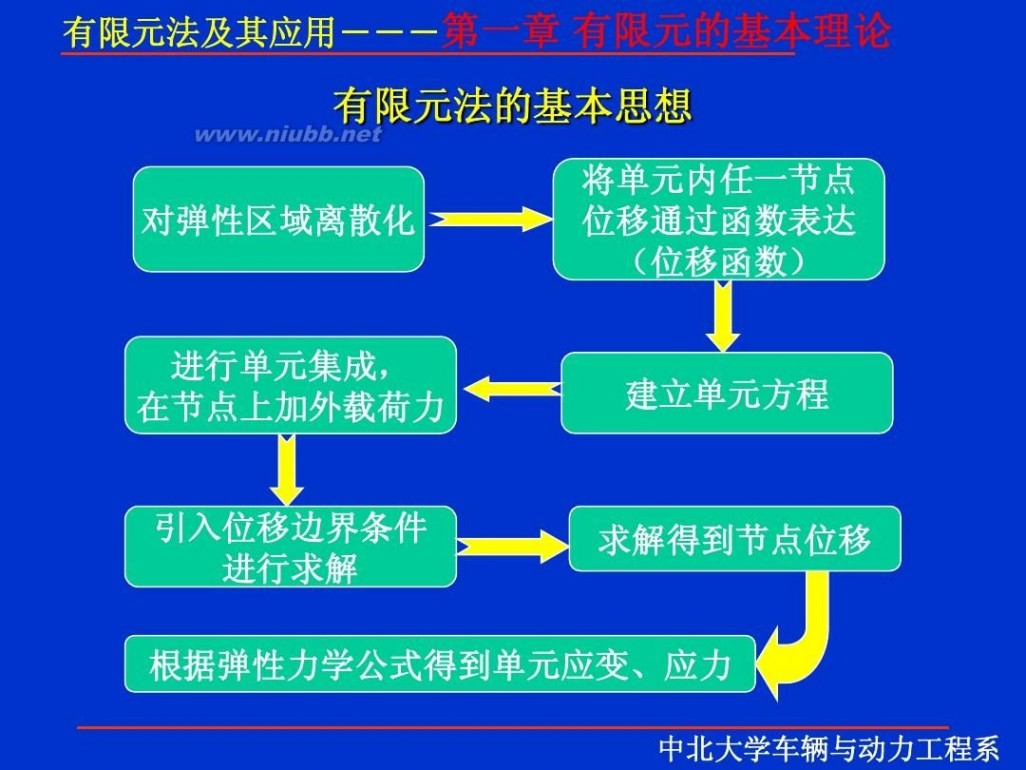
有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
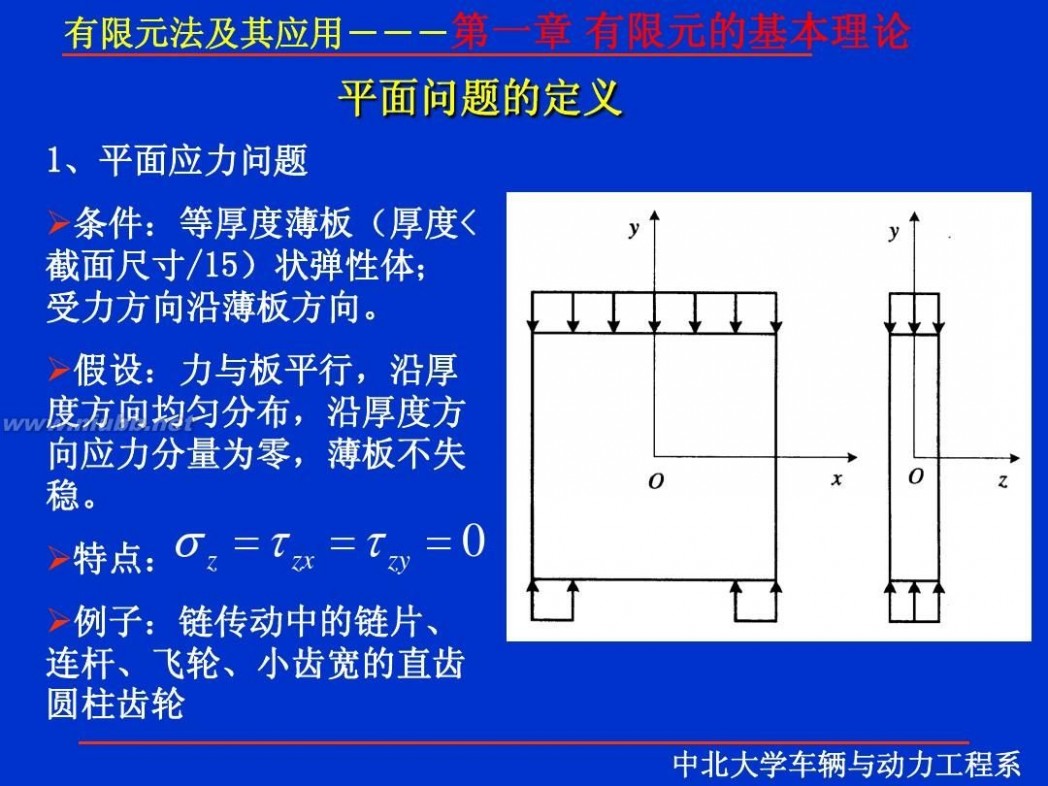
有限元 有限元理论
有限元 有限元理论
有限元 有限元理论
有限元 有限元理论
有限元 有限元理论
有限元 有限元理论
有限元 有限元理论
有限元 有限元理论
有限元 有限元理论

有限元 有限元理论
有限元 有限元理论
有限元 有限元理论

有限元 有限元理论
有限元 有限元理论
有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
有限元 有限元理论

有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
有限元 有限元理论

有限元 有限元理论
有限元 有限元理论
有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
有限元 有限元理论
有限元 有限元理论

有限元 有限元理论
有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
有限元 有限元理论
有限元 有限元理论
有限元 有限元理论
有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
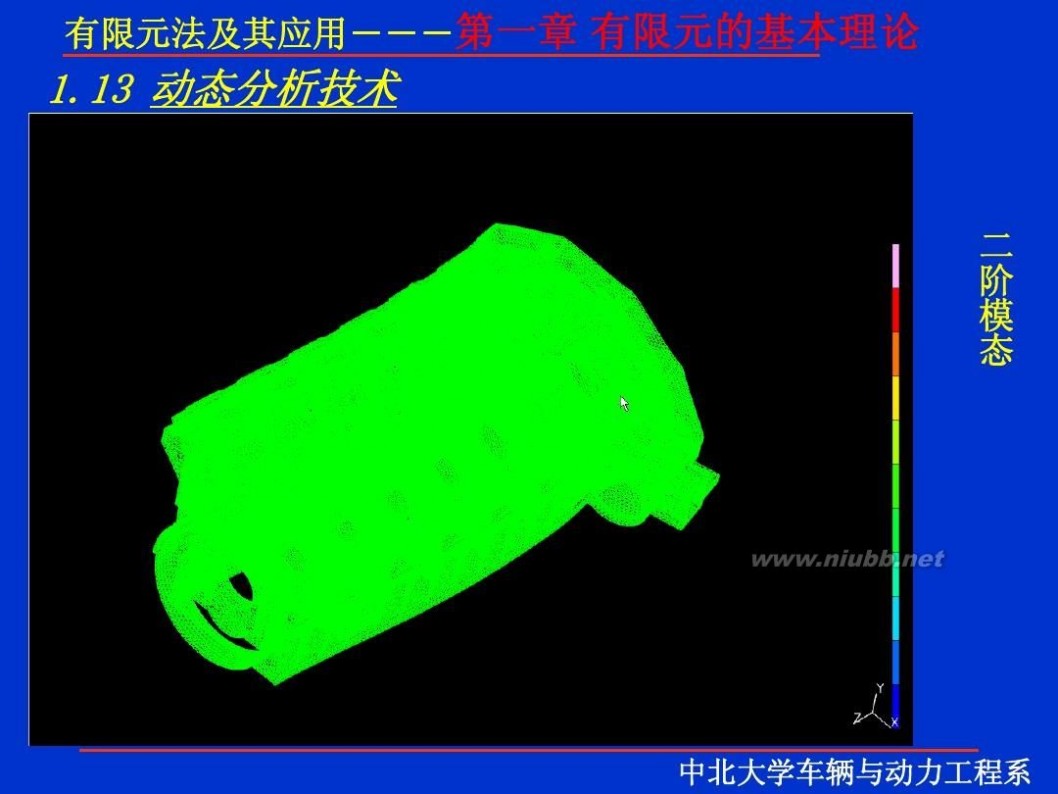
有限元 有限元理论

有限元 有限元理论

有限元 有限元理论
二 : 有限元分析论文
用有限元分析Hyperworks结构
机制1091 19号 何志强
论文关键词:
拓扑优化 形状优化 精密铸造 后悬置支架 有限元分析
论文摘要: 本文主要阐述借助于Alatir公司的Hyperworks结构优化软件,对精密铸造产品进行结构优化设计,且以对某汽车驾驶室后悬置支架的结构优化为例,着重介绍了拓扑优化和形状优化在精密铸造产品结构设计上的应用方法及功能。事实表明拓扑优化和形状优化的联合应用,对精密铸造产品的结构设计起到非常关键的帮助作用,最后通过此软件对优化后的产品结构进行有限元分析,验证优化后产品结构的强度和刚度。
HyperWorks在精密铸造产品优化设计中的应用
一、引言
在当前的汽车工业中,减轻设计重量和缩短设计周期是两个突出的问题,在传统的设计中,由于机械产品机构的复杂性,长期以来主要应用经验类比设计,对产品结构作定性分析和经验类比估算,在决定实际结构时,一般都取较大的安全系数,结果使得产品都是“傻”、“大”、“粗”,使材料的潜力得不到充分发挥,产品的性能也得不到充分的把握。所以传统的汽车设计思路已经不能满足当前设计的需要。汽车轻量化设计开始占据了汽车发展中的主要地位,它既可以提高车辆的动力性,降低成本,减少能源消耗又能减少污染。但是,简单的汽车轻量化设计却是一把双刃剑,它在减轻汽车重量的同时,也牺牲了车辆的强度和刚度,甚至对产品的结构寿命也产生影响,在此情况下,有限元分析方法在汽车设计中的合理应用就得到了充分体现,经过近几年的实践证明,Altair公司的有限元分析技术以及拓扑优化技术在汽车行业获得了非常成功的应用。特别是对于一些结构复杂的汽车铸造结构件,Hyperworks 的有限元分析技术、拓扑优化和形状优化技术的推广使得材料的潜能及铸造的优势得到了充分的发挥。
本文将详细介绍利用Hyperworks的拓扑优化和形状优化技术对东风商用车驾驶室后悬置支架进行减重优化设计的应用过程。以及如何应用Hyperworks验证改进结构后的应力和应变情况,使该后悬置支架减重优化后的结构能够满足产品的使用性能和铸造工艺性要求。
二、有限元法的概念和优化设计流程确立
2.1有限元法和有限单元的概念
有限元法又称有限单元法,是结构分析的一种数值计算方法,它随着计算机的发展而应运而生,并得到了广泛应用,目前已成为工程数值分析的有力工具。在实际工程应用中,我们首先把CAD模型分割成有限个实体或者壳单元。一般作为实体单元所适合的结构,是具有三维形状变化的物体,不太适合棒状、平板状的物体。实体单元是利用3D-CAD所作
好的实体模型,能够拿来就能作有限元模型处理,这一点非常方便。 但是用实体单元制成的模型,因为节点数往往较多在分析时务必注意计算机磁盘用量和计算时间。
另外从实体单元能够把三维图形原封不动地适用于结构分析的模型上这一点来说,对于结构复杂的零件,采用实体单元是很好用的单元。实体单元有六面体、五面体、四面体,在用自动生成的情况下使用四面体较多。从分析精度而言,使用六面体为好,自动生成的三维形状也有必须限制用于六面体的等等,五面体单元在评价应力时尽量不使用此方法为好。壳单元有三角形和四边形单元,对于板单元尽量使用四边形单元,对于实体单元尽量使用六面体单元。使用三角形或四面体单元与使用四边形或六面体单元时相比有使结构增加刚性的模型化倾向。在本文我们所做的驾驶室后悬置支架的优化计算中,由于结构和受力状况的复杂性,我们采用实体单元与壳单元相结合的划分方法。
2.2 确立优化设计流程
在利用Hyperworks软件做优化分析时,通常的流程是首先读入CAD模型,然后划分网格,添加边界条件,设置优化分析模型参数。优化分析模型一般是由目标函数、约束条件、优化设计变量三个方面组成,借助于Hyperworks软件的OptiStruct模块,对于后悬置支架的轻量化设计,在现有的计算机条件下可以很方便的实现。首先,在轻量化分析过程中,一般选取优化设计变量为支架的体积的减少量,然后采用传统的拓扑优化方法,将总体的应变能作为目标函数。在本次后悬置支架的优化分析中,主要采用OptiStruct模块的拓扑优化和形状优化。首先,拓扑优化可以获得一个最佳的结构布局——即最佳的材料分布;然后在这个最优结构布局的基础上按照实际设计需求形成一个新的设计方案,并反馈到CAD软件中,形成新的CAD模型,最后应用更仔细的形状优化工具,同时添加适合铸造的约束条件,得到最有效的细节设计方案。
图(1)代表了该后悬置支架的简单优化设计流程,从最初的模型导入,以及之后的约束条件与目标函数的设定,同时包括制造工艺参数的设定,最后通过形状优化得到的最终设计方案。


根据优化需求,将三维模型进行非安装部位的材料填充导入三维模型

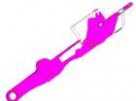


3.1有限元模型建立
3.1.1后悬置支架原始结构分析
由于驾驶室后悬置系统布置方式比较复杂,整个驾驶室后悬置系统由安装于浮动横梁上的左右各一个橡胶缓冲块支撑,两个悬置支架对称的垂直立于车架大梁上,中间用一弧型横梁连接,在悬置支架的两侧对称的布置两个筒式减震器,而本文所要优化分析的后悬置支架是整个系统中受力最为复杂的关键零件。该零件在原始设计中,由于整个机构的复杂性,对产品的性能未能充分把握,在进行设计时只能作定性分析和类比估算,确定实际结构时,选择的安全系数过大,致使设计出来的产品结构过于笨重,粗大,缺乏美观。另外,由于对实际的受力点未能牢牢把握,导致结构材料分布不够均匀,铸造工艺性较差。原始结构见图(2)


图(2)原始结构模型图
3.1.2 有限元网格划分
有限元网格划分是进行有限元优化分析至关重要的一步,有限元分析的精度和效率与网格单元的密度和几何形状有着密切的关系,并且有限元网格划分的好坏,对后续数值计算结
果的精确性有着直接的影响,它不但涉及单元的形状及其拓扑类型、单元类型还有选择什么样的网格生成器、网格密度的定义、单元的编号以及几何体元素等等。所以在实际应用中,选择合理的网格单元对整体模型的分析有重要的影响。根据上述介绍,结合后悬置支架结构的复杂程度以及优化分析的要求,对其采用实体单元网格划分,同时,在非干涉和装配部位进行必要的材料填充;另外,对分析过程中涉及到的弧形横梁因结构简单,属于简化梁结构,故采用壳单元的划分方式


具体网格划分见图(3)
后悬置支架弧型横梁
图(3)有限元网格模型
其节点数和单元数见表(1)
表(1)后悬置支架及横梁的节点与单元数
表(1)后悬置支架及横梁的节点与单元数

3.2 确定边界条件及设置优化参数
3.2.1 确定边界条件
由于驾驶室后悬置系统是以垂直方式布置,在车辆高速行使时,路面通过悬挂系统传递到驾驶室的冲击,发动机、传动系传递到驾驶室上的振动,以及侧向减振器所带来的瞬时冲击,是我们分析时主要考虑的因素。
计算时考虑驾驶室受垂知方向4G(瞬时),侧向2.5G(稳态)的冲击,同时对支架底端与
车架大梁连接处用螺栓固定,该产品受力工况及约束条件如下图(4)所示

图(4)后悬置支架受力工况
3.2.2材料属性及性能参数
该后悬置支架采用ZGD410-700制成,其材料参数如表(2)所示。
表(2) 车身后悬置支架材料参数

四、拓扑优化和形状优化
4.1车身后悬置支架的拓扑优化
拓扑优化就是在产品初时设计阶段,利用优化计算得到满足设计要求的结构外形,并且可以返回到CAD,进行详细的结构设计,然后再利用形状或尺寸优化调整细节,最终得到满足要求的设计方案。对于这个后悬置支架的拓扑优化,主要问题是怎样使支架结构合理布置,以及如何最好的模拟支架所受的垂直载荷和侧向载荷。
在本次拓扑优化过程中,采用后悬置支架与横梁整体分析,但对后悬置支架单独优化的方式,这样获得的结果更趋近于真实的情况。由于拓扑优化对加强筋及凸缘刚度的敏感性较高,因此在采用传统的拓扑优化方法,定义设计变量时,将体积和应变能作为目标响应,设计空间的体积减少量作为优化的约束条件,总体的应变能作为最终的目标函数,这里的总体应变能不仅包括设计空间的应变能,同时也包括非设计空间的应变能。
最后,根据拓扑优化结果云图,返回CAD模型,结合精密铸造工艺,尽可能的凸出筋骨,
减少大平面,在遵循实体最小原则下重新进行三维设计造型。优化云图及结构优化方案见图
(5)

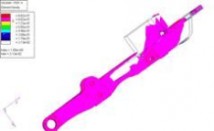
拓扑优化云图(二)

结构优化方案
图(5)拓扑优化云图和结构优化方案
4.2 车身后悬置支架的形状优化

根据以上拓扑优化结果,确定了一个在给定载荷
条件下满足设计要求的最佳结构布置方案,在此方案的基础上,对后悬置支架进行细节优化——形状优化,在形状优化中,同时要考虑结构应力和屈曲变形。理论上为了突出筋骨,保持整个结构布置的均匀化,同时减少局部应力的集中,我们只对该有限元模型做局部形状优化,如图(7)所示,这样就避免整体优化时间上的浪费。
为形状优化建立了有限元模型之后,我们要将适合铸造的工艺参数、应力标准和屈曲要求作为形状优化的设计约束,将质量最小化设为设计目标函数,对于应力约束,设计约束不允许该处的最大应力超出材料的屈服极限,同时在实际优化过程中,该处结构的厚度只能要求向内侧移动,高度只能向上移动。最终经过形状优化后结构见

图(8)形状优化后最终结构图
五、结构验证与对比分析

经过拓扑优化和形状优化,我们最终得到
了较为理想的设计方案,为了验证该优化方案的可靠性,特对此机构进行有限元分析计算,同时对用传统的经验类比方法设计的优化方案进行分析对比。用传统经验类比方法设计的方案如图(9)传统优化设计方案
结合实际受力情况对传统优化设计方案和拓扑优化方案分别做有限元验证分析,应力云图见图(


10
传统优化设计方案应力云图 拓扑优化方案应力云图
图(10)方案验证应力云图
由以上分析可知,传统优化设计方案最大应力高达726MPa,出现在台肩处,而拓扑优化方案的最大应力虽然达到576MPa,但是位置出现在弧型横梁上,与传统优化设计方案相比,相同位置的最大应力由710MPa减少到216MPa。其对比参数见表(3):
表(3)优化前后结构性能对比

六、结束语
经过上述优化方案的对比,我们可以很清楚的看到,利用传统的优化方式和利用Hyperworks的拓扑和形状优化方式的差别,虽然重量相差不多,分别下降了35%和35.5%,但是在同种工况作用下,传统方式优化的产品结构多处应力超出材质屈服极限,且最大应力达到了726MPa,远远超出了材料的屈服极限,在使用过程中很容易就发生断裂;而采用Hyperworks的拓扑和形状优化方式优化的产品结构最大应力只有230MPa,低于所使用材质的屈服极限410MPa,且同一部位由传统优化结构的710MPa减少到218MPa,同比强度增加了2.65倍,刚度增加了1.27倍,并且优化后的产品结构更适合于铸造工艺。
由上述可知,车身后悬置支架的优化设计验证了HyperWorks软件的OptiStruct模块在精密铸造产品的成功应用,说明了此技术在工业制造中具有非常优秀的特点,打破了生产单位不能独立改善产品结构的历史。随着工业产业的发展,OptiStruct的优化概念将会被越来越多的人接受并有效运用,届时它将真正成为产品结构设计工程师的左膀右臂。
参考文献
1、张国瑞 有限元法 北京 机械工业出版社 1991
2、刘惟信 机械最优化设计(第二版) 北京 清华大学出版社 1994
3、孙靖民 梁迎春 陈时锦 机械结构优化设计 哈尔滨 哈尔滨工业大学出版社 2004
4、于开平 周传月 谭惠丰 HyperMesh从入门到精通 北京 科学出版社 2005
三 : 19研究生课程论文《非线性有限元分析》
1 引言
在科学技术领域内,对于许多力学问题和物理问题,人们已经得到了它们所应遵循的基本方程(常微分方程或偏微分方程)和相应的定解条件(边界条件)。但能够用解析方法求出精确解的只是少数方程性质比较简单,并且几何形状相当规则的问题。对于大多数工程实际问题,由于方程的某些特征的非线性性质,或由于求解区域的几何形状比较复杂,则不能得到解析的答案。这类问题的解决通常有两种途径。一是引入简化假设,将方程和几何边界简化为能够处理的情况,从而得到问题在简化状态下的解答。但是这种方法只是在有限的情况下是可行的,因为过多的简化可能导致误差很大甚至是错误的解答。因此人们多年来一直在致力于寻找和发展另一种求解途径和方法——数值解法。特别是五十多年来,随着电子计算机的飞速发展和广泛应用,数值分析方法已成为求解科学技术问题的主要工具。
已经发展的数值分析方法可以分为两大类。一类以有限差分法为代表,主要特点是直接求解基本方程和相应定解条件的近似解。其具体解法是将求解区域划分为网格,然后在网格的结点上用差分方程来近似微分方程,当采用较多结点时,近似解的精度可以得到改善。但是当用于求解几何形状复杂的问题时,有限差分法的精度将降低,甚至发生困难。
另一类数值分析方法是首先建立和原问题基本方程及相应定解条件相等效的积分提法,然后再建立近似解法并求解。如果原问题的方程具有某些特定的性质,则它的等效积分提法可以归结为某个泛函的变分,相应的近似解法实际上就是求解泛函的驻值问题。诸如里兹法,配点法,最小二乘法,伽辽金法,力矩法等都属于这一类方法。但此类方法也只能局限于几何形状规则的问题,原因在于它们都是在整个求解区域上假设近似函数,因此,对于几何形状复杂的问题,不可能建立合乎要求的近似函数。
1960年,R.W.CLOUGH发表了有限单元法的第一篇文献“The Finite Element Method in Plane Stress Analysis”,这同时也标志着有限单元法(FEM)的问世。有限单元法的基本思想是将连续的求解区域离散为一组有限个,且按一定方式相互联接在一起的单元的组合体。由于单元能按不同的联结方式进行组合,且单元本身又可以有不同形状,因此可以模型化几何形状复杂的求解域。并且可以利用在每一个单元内假设的近似函数来分片地表示全求解域上待求的未知场函数,从而使一个连续的无限自由度问题变成离散的有限自由度问题。
现已证明,有限单元法是基于变分原理的里兹法的另一种形式,从而使里兹法分析的所有理论基础都适用于有限单元法,确认了有限单元法是处理连续介质问题的一种普遍方法。利用变分原理建立有限元方程和经典里兹法的主要区别是有限单元法假设的近似函数不是在全求解域而是在单元上规定的,而且事先不要求满足任何边界条件,因此可以用来处理很复杂的连续介质问题。
在短短四十余年的时间里,有限单元的分析方法已经迅速地发展为适合于使用各种类型计算机解决复杂工程问题的一种相当普及的方法。如今,有限元广泛地应用于各个学科门类,已经成为工程师和科研人员用于解决实际工程问题,进行科学研究不可或缺的有力工具。有限单元法的应用范围已由弹性力学平面问题扩展到空间问题,板壳问题,由静力平衡问题扩展到稳定问题,动力问题和波动问题。分析的对象从弹性材料扩展到塑性,粘弹性,粘塑性和复合材料等,从固体力学扩展到流体力学,传热学等连续介质力学领域。在工程分析中的作用已从分析和校核扩展到优化设计并和计算机辅助设计技术相结合。各种各样商业化的大型通用有限元软件层出不穷,不断推陈出新。可以预见,随着现代力学,计算数学,计算机技术等学科的发展,有限单元法作为一个具有巩固理论基础和广泛应用范围的数值分析工具,必将得到进一步的完善和发展。
2 非线性问题的类型和求解特点
2.1 非线性问题的类型
2. 1. 1 线性分析的含义
在有限元分析中的线性假设包含下列含义:即结点位移为无限小量,材料为线弹性,加载时边界条件的性质保持不变。于是,静力平衡方程可以表示为:
?K??U???R? (2.1)
其中,?K?为刚度矩阵,?R?为荷载矢量。由于?K?和?R?的元素为常数,故位移响应?U?是荷载矢量?R?的线性函数。也就是说,如果?R?变为??R?,则?U?变为??U?,其中,?为常数。这就是所谓的线性有限元分析。如果上述假设中的任何一条不能得到满足,那么就属于非线性有限元分析。
2. 1. 2 非线性分析的必要性
结构力学问题,从本质上讲都是非线性的,线性假设只是实际工程问题的一种简化。当然,任何实际工程问题的求解都避免不了适当地简化,简化是否合理主要应根据求解效果和实际经验来判断。对于目前工程实际中的很多问题,如地震作用下结构的弹塑性动力响应,高层建筑抗风,大跨度网壳结构动力稳定性,索膜结构找形荷载与裁减分析,大型桥梁风致振动等问题的研究,仅仅假设为线性问题是很不够的,常常需要进一步考虑为非线性问题。因此,对各种工程结构的非线性分析就是必不可少且日趋重要了。对于结构力学的非线性问题来说,有限单元法是最为有效的数值分析方法。
2. 1. 3 非线性问题的类型
通常,把非线性问题分为两大类,即分为几何非线性和材料非线性。但从建立基本方程和程序设计的方便出发,又可分为三种类型:
1.材料非线性:非线性效应仅由应力应变关系的非线性引起,位移分量仍假设为无限小量,故仍可采用工程应力和工程应变来描述,即仅材料为非线性。非线性的应力应变关系是结构非线性的常见原因,许多因素都可以影响材料的应力应变性质,包括加载历史(如在弹塑性响应状况下),环境状况(如温度),加载的时间总量(如在蠕变响应状况下)等。
2.几何非线性:如果结构经受大变形,则变化了的几何形状可能会引起结构的非线性响应,这又可以分为两种情形:
第一种情形,大位移小应变。只是物体经历了大的刚体平动和转动,固连于物体坐标系中的应变分量仍假设为无限小。此时的应力应变关系则根据实际材料和实际问题可以是线性的也可以是非线性的。
第二种情形,大位移大应变。也即最一般的的情况,此时结构的平动位移,转动位移和应变都不再是无限小量,本构关系也是非线性的。
3.状态非线性:除以上两种非线性问题之外,还有一种非线性问题,即由于系统刚度和边界条件的性质随物体的运动发生变化所引起的非线性响应。例如,一根只能拉伸的钢索可能是松散的,也可能是绷紧的;轴承套可能是接触的,也可能是不接触的; 冻土可能是冻结的,也可能是融化的。这些系统的刚度和边界条件由于系统状态的改变在不同的值之间突然变化。状态改变也许和载荷直接有关,也可能由某种外部原因引起。最为典型的就是接触问题,接触是状态非线性类型中一个特殊而重要的子集。通常情况下,状态非线性问题可以在上述材料非线性和几何非线性类型中的每一种同时出现,从而使得问题的分析变得更为复杂。
2.2 非线性问题的求解特点
2. 2. 1 非线性分析的基本问题
非线性分析的基本问题是求出在当前荷载作用下的平衡状态。如果作用的荷载被描述成时间的函数,则物体有限元离散系统的平衡方程可以表示为:
t?R??t?F??0 (2.2)
t其中,矢量?R?由t时刻外荷载的结点力分量所构成,而矢量?F?则表示t时刻的单元应力所引t
起的结点力分量。平衡方程(2.2)应针对t时刻的几何位形建立,并应计入所有的非线性效应。如果是动力分析,矢量?R?中还应当包括惯性力和阻尼力。 t
在求解非线性问题时,(2.2)式应在全部加载历史中成立。变量t的引入并不意味着一定是动力问题。在静力分析中,t不具有真实“时间”的含义,它的不同取值只是表示相应于不同位形的不同的荷载水平。但是,在动力分析或具有时间效应的静力分析中,变量t就有了它本来的“时间”的含义。
2. 2. 2 非线性方程组的增量逐步解法
对于许多工程结构,我们所关心的常常是在特定的荷载水平下,或相应的时间物体中的应力和变形。实际问题根据其解法可以分为两大类型。第一类问题无需计算中间变形过程,可直接求解在给定荷载下的平衡位形。但是,如果问题的几何性质或材料性质与路径相关或与时间相关,即该问题依赖于变形历史,则中间变形过程的计算是不可缺少的,这就是第二类问题。从本质上来说,非线性问题是第二类问题。此时,往往采用增量分析的方法。
增量逐步解法的基本思想是:假定t时刻的解为已知,要求t+Δt时刻的解,其中,Δt是适当选择的时间增量。在t+Δt时刻,式(2.2)写成为:
t??t?R??t??t?F??0 (2.3)
?F??t?F???F? (2.4) 这里,左上标表示为t+Δt时刻的量。由于t时刻的解为已知,因此,可以写为: t??t
式中,?F?表示t到t+Δt时间间隔内,由于单元内应力增量所引起的结点力增量矢量。这一矢量可以近似表示为:
?F??t?K??U? (2.5)
U?为Δt时间间隔中的结点位移增式中,?K?为相应于t时刻材料和几何条件的切线刚度矩阵。?t
量,现在它还是未知的。将式(2.4)和(2.5)代入式(2.3)中,得到:
t?K??U??t??t?R??t?F? (2.6)
t??t上式中只有位移增量?U?为未知,一旦解出,即可算得t+Δt时刻的位移: ?U??t?U???U? (2.7)
t??t根据?U?,就容易算出t+Δt时刻的应力及t??t?F?,t??t?K?,于是马上可以着手下一步的计算。但要指出的是,式(2.5)是一个近似表达式,因此t+Δt时刻的解也是近似的,如果急于求成的作下去,最终结果可能出现不可忽视的重大误差以致于达到荒谬的地步。解决这一困难的办法是以花费计算时间为代价,即在t到t+Δt时步中进行足够次数的迭代,以保证最终的解获得足够的精度。
2. 2. 3 引入修正Newton-Raphson迭代格式的增量逐步解法
现在更多采用的方法是在每一个荷载增量步中,使用Newton-Raphson迭代法或修正的Newton-Raphson迭代法。由于后者不需要每次迭代时都计算切线刚度矩阵,因此在实际中具有更广泛的应用。现对该方法做简单的介绍。
在t时刻到t+Δt时刻的时步中,修正Newton-Raphson法的迭代公式可以表示为:
t?K???U??i??t??t?R??t??t?F??i?1? (2.8)
?U??i??t??t?U??i?1????U??i? (2.9)
t??tt??t其中,i表示迭代步数,依次取1,2,3,?,其迭代所用的初始值正是t时刻的解,即: t??t?U??0??t?U?,?F??0??t?F? (2.10)
式(2.8)的右端项:t??tt??t?i?1?在迭代过程中,?F??R??t??t?F??i?1? 称为第i步迭代前的不平衡荷载。
随i的增加而逐步接近t??t?R?。因此,我们可事先对不平衡荷载的模给定一个精度指标,每次迭
t??t代后检查不平衡荷载是否小于该指标。若满足精度,则在求出
否则继续迭代,直到满足精度要求为止。
?U?之后转入下一时步的计算,
3 材料非线性问题的有限单元法
3.1 材料非线性问题概述
在所有的非线性分析问题中,材料非线性问题的处理相对简单,不需要重新列出整个问题的表达格式,只要将材料本构关系线性化,就可将线性问题的表达格式推广用于非线性分析。一般来说,通过试探和迭代的过程求解一系列线性问题,如果在最后阶段,材料的状态参数被调整得满足材料的非线性本构关系,则最终可得到问题的解答。
材料非线性问题可以分为两种类型。一类是不依赖于时间的弹塑性问题,其特点是当荷载作用以后,材料变形立即发生,并且不再随时间而变化。另一类是依赖于时间的粘(弹,塑)性问题,其特点是荷载作用以后,材料不仅立即发生变形,而且变形随时间继续变化。在荷载保持不变的条件下,由于材料粘性而继续增长的变形称之为蠕变;另一方面,在变形保持不变的条件下,由于材料粘性而使应力衰减称之为松弛。显然,后一类材料非线性问题在求解时更为困难一些。
3.2 材料非线性本构关系
限于篇幅,本文仅讨论最为常见的弹塑性非线性本构关系。弹塑性材料进入塑性的特征是当
荷载卸去以后存在不可恢复的永久变形,因而在涉及卸载的情况下,应力应变之间不再存在惟一的对应关系,这是区别于非线弹性材料的基本属性。以材料的单向受力情况为例,只是在加载时应力应变呈现非线性关系,还不足以判定材料是非线性弹性还是弹塑性。但是一经卸载立即发生两者的区别,非线性弹性材料将沿原路径返回,而弹塑性材料将依据不同的加载历史卸载后产生不同的永久变形。
任何一种弹塑性材料都应当满足塑性力学的四条基本准则,这里对此作简单的介绍:
1. 初始屈服条件:规定了材料开始塑性变形的应力状态。在有限元分析中,通常采用V.Mises
准则。
2. 流动准则:规定塑性应变增量的分量和应力分量以及应力增量分量之间的关系。
3. 硬化准则:规定材料进入塑性变形后的后继屈服函数。对于理想弹塑性材料,因无硬化
效应,后继屈服函数和初始屈服函数一致;对于硬化材料,通常又有各向同性硬化准则,随动硬化准则和混合硬化准则三种不同的准则。
4. 加载,卸载准则:用以判别从一塑性状态出发是继续塑性加载还是弹性卸载,这是计算
中判定是否继续塑性变形以及决定是采用弹塑性本构关系还是弹性本构关系所必须的。 各种类型的弹塑性材料可以从对各自的后继屈服函数进行微分出发,进而推导出各自相应的应力应变的增量关系,这里不一一列举。
需要进一步说明的是,对于处于高温条件下工作的结构,必须考虑温度对本构关系的影响。比如随着温度的升高,屈曲极限有所降低,材料硬化特性也有所减少,并逐渐接近理想塑性材料,同时材料常数E,μ,α等也随温度变化而有所变化。至于长期工作在高温条件下的结构还必须考虑蠕变的效应。
3.3 材料非线性问题的有限元表达格式
对于弹塑性材料,由于材料和结构的弹塑性行为与加载以及变形的历史有关。因此,在进行结构的弹塑性分析时,通常将荷载分成若干个增量,然后对于每一荷载增量,将弹塑性方程线性化,从而使弹塑性分析这一非线性问题分解为一系列的线性问题。
按照这种思想,首先建立增量形式的荷载条件和位移条件,进而建立增量形式的虚位移原理,即增量形式的最小势能原理,最终即可得到基于增量形式的有限元表达格式。系统平衡方程形式同前(3.5)式,其中切线刚度矩阵?K?在这里是系统的弹塑性刚度矩阵。 t
弹塑性增量有限元分析在将加载过程划分为若干增量步以后,对于每一个增量步应包含下列三个算法步骤:
1. 线性化弹塑性本构关系,并形成增量有限元方程。
2. 求解有限元方程。注意在求解过程中每个增量步或每次迭代时弹塑性刚度矩阵都可能发
生局部的变化。
3. 积分本构方程,决定新的应力状态,检查平衡条件,并决定是否进行新的迭代。
上述每一步骤的算法方案和数值方法,以及荷载增量步长的选择都关系到整个求解过程的稳定性,精度和效率。这里尤其需要注意的是非线性方程组求解方案的选择。
通常可以采用以下几种求解方案:无迭代的增量解法,具有变刚度迭代(N-R迭代)的增量解法和具有常刚度迭代(mN-R迭代)的增量解法。变刚度迭代具有良好的收敛性,允许采用较大的时间步长,但每次迭代都要重新形成和分解新的刚度矩阵。而采用常刚度迭代可以节省上述计算费用,缺点是收敛速度较慢,特别在接近荷载的极限状况时,因此经常需要同时采用加速迭代的措
19研究生课程论文《非线性有限元分析》_有限元分析论文
施。具体采用何种求解方案,应根据具体问题的特点,综合考虑精度和效率两方面因素。
对于除弹塑性以外的材料非线性问题,例如热弹塑性—蠕变问题,粘弹塑性问题等,由于同时涉及独立于时间和依赖于时间的两类非弹性变形以及本构方程的高度非线性,无论是其本构方程的建立和它的积分方法,还是非线性方程组的求解方法都远比通常的弹塑性分析困难得多。但还是有很多共性的方面,这里不再展开详述。
4 几何非线性问题的有限单元法
4.1 几何非线性问题概述
在某一固体力学问题中,如果假定物体所发生的位移远小于物体自身的几何尺度,应变远小于1,那么此问题就称作满足“小变形假定”。在此前提下,建立物体或微元体的平衡条件时可以不考虑物体的位置和形状(简称位形)的变化。因此分析中不必区分变形前和变形后的位形。同时在加载和变形过程中的应变可用一阶无穷小的线性应变进行度量。
但是在实际中,我们往往会遇到很多不符合小变形假定的问题,例如板壳等薄壁结构的屈曲问题。此时必须考虑变形对平衡的影响,即平衡条件应建立在变形后的位形上,同时应变表达式也应包括位移的二次项。这样一来,平衡方程和几何关系都将是非线性的。这种由于大平动和大转动引起的非线性问题称为几何非线性问题。几何非线性问题还有另外一种类型,例如金属的成型,橡皮型材料受荷载作用,都可能会出现很大的应变,这时除了采用非线性的平衡方程和几何关系以外,还需要引入相应的应力应变关系,尽管对于后一问题材料通常还处于弹性状态。当然大多数大应变问题是和材料的非弹性性质联系在一起的。这类几何非线性问题即通常所说的大平动,大转动,大应变问题。
4.2 几何非线性问题的有限元表达格式
早期几何非线性有限元分析基本上是线性分析的扩展,针对各个具体问题分别进行分析。而近年来,基于非线性连续介质力学原理的有限元分析取得很大发展,得到了统一的一般非线性分析的表达格式。
基于非线性连续介质力学,首先应当对大变形情况下的应变和应力进行度量。这是因为在非线性问题中,由于存在的大位移,大应变而导致有限变形,使得原来传统的小变形下的Cauchy方程不再适用。此时,根据连续体在不同的位形下坐标的变换,对变形前后物体上某一线段变形的度量可以采用两种不同的应变度量方式。即用变形前坐标表示的Green应变张量和用变形后坐标表示的Almansi应变张量。在大变形问题中,是用从变形后的物体内截取出的微元体来建立平衡方程和与之等效的虚功原理的。因此,在从变形后物体内截取出的微元体上面定义的应力张量称为Euler应力张量。如果用于变形前的位形,可以具体定义另外两种应力张量:Lagrange应力张量和Kirchhoff应力张量。此外,在连续介质力学中还定义了一种其分量不随材料刚体转动而变化的速率型应力张量,Jaumann应力速率张量。
在涉及几何非线性问题的有限单元法中,通常都采用增量分析的方法。为了得到方程的解答,所有的变量都应参考某一已经求得的平衡位形。在实际分析中,通常有以下两种选择:
1.全Lagrange格式(Total Lagrange Formulation,简称T.L.格式),这种格式中所有变量以时间0的位形作为参考位形。
2.更新Lagrange格式(Updated Lagrange Formulation,简称U.L.格式),这种格式中所有变量以时间t的位形作为参考位形。因为在求解过程中参考位形是不断改变的,所以称之为更新的
Lagrange格式。
由以上两种格式导出的求解方程在理论上是等效的,如若采用数学上相一致的本构关系,它们将产生相同的结果。但在求解的有限元矩阵方程本身和求解步骤上仍有一定的差别。在通用的有限元程序中,通常同时包括这两种格式,使用时可以根据所分析问题及材料本构关系的具体特点和形式选择最有效的格式。
为进一步说明非线性分析的特点,下表列出按非线性问题的不同分类所采用的不同描述方法和应力应变。
表1 非线性问题分类
4.3 几何非线性问题有限元方程的求解
对于几何非线性有限元的求解,一般采用等参元对求解域进行离散。两种表达格式T.L.和 U.L.都可应用,关键在于对求解方程的线性化处理。因为无论是T.L.格式还是 U.L.格式,都是基于线性化处理后的虚位移原理建立的有限元矩阵方程,该矩阵方程仅是对于每一时间步长所应求解的非线性方程的近似。由于系统的非线性性质,线性化处理带来的误差将可能导致解的漂移或不稳定。因此,仍需采用基于Newton-Raphson迭代格式或修正Newton-Raphson迭代格式的增量逐步解法求解方程组。
在实际分析中,两种格式用于求解的时间一般情况下相差不多,究竟选择哪种格式通常取决于所采用的本构关系的具体形式。也就应当在求解之初便首先区分是大应变还是小应变,选择格式已在表1中列出,此处不再详述。
和材料非线性问题相比,几何非线性问题有着更为复杂多样的荷载—位移路径,如在荷载控制下的疾速通过和位移控制下的疾速通过。因此,荷载增量步长的自动选择就显得格外重要。近些年来,广泛应用的一类荷载增量步长的自动选择方法是“广义弧长法”。在广义弧长法中,用于调节荷载增量和位移增量在弧长ΔL中作用的比例因子α对弧长法的总体性能有很大的影响。一般采用的比例因子有:α=1的球面弧长法,α=0的柱面弧长法,α=Sp的椭圆弧长法。对于不同的结构和荷载情况,很难说以上α不同取值的三种情况中哪一种具有绝对的优势,但是α=0的柱面弧长法具有较好的普遍适应性。
5 杆索非线性有限元理论
在结构非线性有限元分析中,最为重要也最为基本的是建立精度适合的各种有限单元列式,并在基于某些假定的基础上推导出其单元刚度矩阵和有限元求解方程。下由于目前的研究和应用中已经出现了相当多的上述单元的理论和模型,限于篇幅并基于应用角度,每种单元仅选择一种最为常用,精度也较高的单元加以介绍。
5.1 非线性有限杆单元理论
5. 1. 1 基本假定
1. 杆单元只能承受轴向力;
2. 杆单元的应力应变关系符合虎克定律; 3. 杆单元位移变形为大位移小应变。 5. 1. 2 刚度矩阵及有限元方程
假定单元位移函数线性插值:u???
?
i??1L???u12
?
?
i?L
?ui ??u??1?u1tt
uii?X2t1
j?Xi,j
????X?1?1??j
t??2?? jL?ui?
L在局部坐标系ξ中,应力应变关系为:??
??Eep??
? 在局部和整体坐标系关系中,转轴时应力增量和应变增量的变换矩阵T为:?T???l2
m2n2lmlnmn?
t
式中:l,m,n是方向余弦。
由此可得:
??
???T?T??? ?????T???? ?????T?ETep?T??????D????
式中:???,???
表示局部坐标系下单元的应变和应力;
???,???表示整体坐标系下单元的应力和应变。
应变增量和位移增量的关系可用[B]矩阵表示,则有限元矩阵可表示为:
?tt
t
K0
???[B
L
]T[D][tBL]tdV
t
V
?t
t
t
Ku
??]T[SE][tB]tdV t
?[B
NLNL
V
?tF???[t
t
B
L
]T[?E]dV
t
V
式中:SE,σE分别为Kirchhoff应力矩阵和向量。
(5.1) (5.2) (5.3)
(5.4)
将积分式展开,得到线性刚度矩阵,非线性刚度矩阵和内力项的矩阵表达式:
??
?l2lmln?
m2mn?lm
?lnmnn2t
tK0??2
?lm?ln??l
??lm?m2?mn?2???ln?mn?n
0?1
?01?
?00tE
?K??A/L?tu
??10?0?1?
?00?
?l2?ln
l2lmln00100?1
?lm?mnlmm2mn?100100
0?10010
?lm?m2
??
?ln?
??mn?
?n2? (5.5)
?ln?mn?
?2n??0?0??
?1? (5.6) ?0?0??1??
t
?F????A??1
t
t
E
?m?nlmn? (5.7)
t??t
u
按虚位移原理的矩阵列式为: 上式即为有限元基本方程。
??K???K????u??
tt
tt
Q?ttF (5.8)
??
5.2 非线性有限索单元理论
索结构在大跨结构中已得到广泛的应用。随着连续长索的不断应用,对于索力学模型的精度要求也越来越高。初期的研究以解析法为基础,对较为简单理想的外荷载和边界条件作了分析。随着计算技术的提高,提出并采用了考虑大变形的各种离散模型,主要有:两节点直线杆单元模型,以等效弹性模量来考虑垂度影响;两节点抛物线索单元模型,以及为了提高分析精度采用内插节点的多节点索单元(三节点,四节点,五节点索单元)模型和采用B样条基构建的索单元模型。下面简要介绍悬链线索单元模型。 5. 2. 1 基本假定
1. 索为理想柔索,不受压且无弯曲刚度; 2. 满足大变形,小应变要求; 3. 索中外荷载沿索长均匀分布。 5. 2. 2 刚度矩阵及有限元方程
作几何非线性分析时,索单元的切线刚度可按下述方法计算。如图1中为一个索单元,其中i点的位移是 ⊿1,⊿2,⊿3;j点的位移是⊿4,⊿5,⊿6;节点力由原来的 F01, F02, F03, F04,F05, F06 增加到F1, F2, F3, F4, F5, F6。此时,节点力及节点位移间的平衡方程式如下:
F4??F1F5??F2
?0??
F6??F3??0L0(假设
)
lx?lx0??1??4?f(F1,F2,F3)
(5.9)
ly?ly0??2??5?g(F1,F2,F3)lz?lz0??3??6?h(F1,F2,F3)
图1 弹性悬链线索单元切线刚度矩阵概念图
在全局坐标系里,悬索上的每一点沿坐标长度方向的微分值如下。如果把这些值整理成荷载和变形的关系,就可已得到柔度矩阵 ([F]),而柔度矩阵的倒数就是刚度矩阵([K])。悬索结构的刚度并不是一次性计算就可得到的,它是通过多次重复计算后,使方程式达到平衡状态时才能得到精确的刚度值。
dlx=dly?dlz?
?f?f?fdF1+dF2+dF3?F1?F2?F3
?g?g?gdF1?dF2?dF3 (5.10) ?F1?F2?F3?h?h?hdF1?dF2?dF3?F1?F2?F3
???f?????F1
?dlx??dF1????g????
?dly???F??dF2?, ??F???
???F1?dl??dF?
?z??3????h
?????F1??
?f
?F2?g?F2?h?F2?f???F3?
?f11f12
?g??
??f21f22?F3??
??f31f32
?h???F3???
?f13??
??f23?? (5.11) ?f33???
???
?dF1??dlx??????1
?dF2???K??dly?, (K?F) (5.12) ?dF??dl??3??z?
柔度矩阵的每个元素可按下式计算:
??fL01F12?11
f11?????lnF?wL?B?lnF?A????????303?wB2?F?wLBA2?FA??F1EA0w?3??03??
f12?
?fFF
??12?F2w
??11
?2?2?
B?F?wLBA?FA??303??
f13?
?fF?F?wL0?BF?A?
??1?23?23? ?F3w?B?F?wLBA?FA?303??
f21?
?g
?f12 (5.13) ?F1
??gL1F22?11
??0??lnF?wL?B?lnF?A????????303?wB2?F?wLBA2?FA? ?F2EA0w?3??03??
f22?
19研究生课程论文《非线性有限元分析》_有限元分析论文
研究生课程论文 非线性有限元分析
?gF2
?f13 ?F3F1
f23?
f31?f32?
?hF?11???1??? ?Fw?BA?1?hF2
?f31 ?F2F1
f33?
?hL1?F?wL0F3???0??3?? ?F3EA0w?BA?
1/2
A??F12?F22?F32?
,
B?F12?F22??F3?wL0?
?
21/2
?
)
则有限元基本方程如下: ?dF??KT?d?? (5.14)
??F1
???
1???F2????1??F3???1
(其中, KT????F
??1???1??F??1???1?
???F1?????1
?F1
??2?F2??2?F3??2????F1??2?F2??2?F3??2
?F1??3?F2??3?F3??3????F1??3?F2??3?F3??3
?F1??4?F2??4?F3??4????F1??4?F2??4?F3??4
?F1??5?F2??5?F3??5????F1??5?F2??5?F3??5
?F1???6?
??F2?
???6??F3?
?
??6??Fii
???F1???Fii
??
??6??F??2???6?
??F3??
???6??
Fij?
) ?Fij??
6 结语
本文简要叙述了非线性有限元分析的若干基本概念和基本原理,掌握这些基本概念和原理对于正确求解工程实际中大量存在的各种形式的非线性问题是至关重要的。同时,随着计算技术的快速发展和计算机硬件性能的不断飞跃,各种大型有限元商业软件不断推陈出新,解决非线性问题的能力越来越强。可以这样认为,工程分析和设计的计算机时代已经来临。也可以这样预言,传统的线弹性分析设计方法在不远的将来必将被非线性的分析设计方法所替代。
主要参考文献:
[1] 张汝清,詹先义.非线性有限元分析[M].重庆: 重庆大学出版社,1990.
[2] K .J .巴特, E. L.威尔逊著;林公豫,罗恩译.有限元分析中的数值方法[M].北京: 科学出版社,1985. [3] K .J .Bathe.Finite Element Procedures in Engineering Analysis, [M].New Jersey: Prentice-Hall,1996. [4] 丁皓江,何福保.弹性和塑性力学中的有限单元法[M].北京: 机械工业出版社,1989. [5] 王瑁成,劭敏.有限单元法基本原理和数值方法[M].北京: 清华大学出版社,1997. [6] 朱伯芳.有限单元法原理与应用[M].北京: 中国水利水电出版社,1998.
[7] 周中坚,卢耀祖.机械与汽车结构的有限元分析[M].上海: 同济大学出版社,1997.
- 11 -
四 : 有限元分析论文
用有限元分析Hyperworks结构
机制1091 19号 何志强
论文关键词:
拓扑优化 形状优化 精密铸造 后悬置支架 有限元分析
论文摘要: 本文主要阐述借助于Alatir公司的Hyperworks结构优化软件,对精密铸造产品进行结构优化设计,且以对某汽车驾驶室后悬置支架的结构优化为例,着重介绍了拓扑优化和形状优化在精密铸造产品结构设计上的应用方法及功能。(www.61k.com]事实表明拓扑优化和形状优化的联合应用,对精密铸造产品的结构设计起到非常关键的帮助作用,最后通过此软件对优化后的产品结构进行有限元分析,验证优化后产品结构的强度和刚度。
HyperWorks在精密铸造产品优化设计中的应用
一、引言
在当前的汽车工业中,减轻设计重量和缩短设计周期是两个突出的问题,在传统的设计中,由于机械产品机构的复杂性,长期以来主要应用经验类比设计,对产品结构作定性分析和经验类比估算,在决定实际结构时,一般都取较大的安全系数,结果使得产品都是“傻”、“大”、“粗”,使材料的潜力得不到充分发挥,产品的性能也得不到充分的把握。所以传统的汽车设计思路已经不能满足当前设计的需要。汽车轻量化设计开始占据了汽车发展中的主要地位,它既可以提高车辆的动力性,降低成本,减少能源消耗又能减少污染。但是,简单的汽车轻量化设计却是一把双刃剑,它在减轻汽车重量的同时,也牺牲了车辆的强度和刚度,甚至对产品的结构寿命也产生影响,在此情况下,有限元分析方法在汽车设计中的合理应用就得到了充分体现,经过近几年的实践证明,Altair公司的有限元分析技术以及拓扑优化技术在汽车行业获得了非常成功的应用。特别是对于一些结构复杂的汽车铸造结构件,Hyperworks 的有限元分析技术、拓扑优化和形状优化技术的推广使得材料的潜能及铸造的优势得到了充分的发挥。
本文将详细介绍利用Hyperworks的拓扑优化和形状优化技术对东风商用车驾驶室后悬置支架进行减重优化设计的应用过程。以及如何应用Hyperworks验证改进结构后的应力和应变情况,使该后悬置支架减重优化后的结构能够满足产品的使用性能和铸造工艺性要求。
二、有限元法的概念和优化设计流程确立
2.1有限元法和有限单元的概念
有限元法又称有限单元法,是结构分析的一种数值计算方法,它随着计算机的发展而应运而生,并得到了广泛应用,目前已成为工程数值分析的有力工具。在实际工程应用中,我们首先把CAD模型分割成有限个实体或者壳单元。一般作为实体单元所适合的结构,是具有三维形状变化的物体,不太适合棒状、平板状的物体。实体单元是利用3D-CAD所作
有限元分析论文 有限元分析论文
好的实体模型,能够拿来就能作有限元模型处理,这一点非常方便。(www.61k.com) 但是用实体单元制成的模型,因为节点数往往较多在分析时务必注意计算机磁盘用量和计算时间。
另外从实体单元能够把三维图形原封不动地适用于结构分析的模型上这一点来说,对于结构复杂的零件,采用实体单元是很好用的单元。实体单元有六面体、五面体、四面体,在用自动生成的情况下使用四面体较多。从分析精度而言,使用六面体为好,自动生成的三维形状也有必须限制用于六面体的等等,五面体单元在评价应力时尽量不使用此方法为好。壳单元有三角形和四边形单元,对于板单元尽量使用四边形单元,对于实体单元尽量使用六面体单元。使用三角形或四面体单元与使用四边形或六面体单元时相比有使结构增加刚性的模型化倾向。在本文我们所做的驾驶室后悬置支架的优化计算中,由于结构和受力状况的复杂性,我们采用实体单元与壳单元相结合的划分方法。
2.2 确立优化设计流程
在利用Hyperworks软件做优化分析时,通常的流程是首先读入CAD模型,然后划分网格,添加边界条件,设置优化分析模型参数。优化分析模型一般是由目标函数、约束条件、优化设计变量三个方面组成,借助于Hyperworks软件的OptiStruct模块,对于后悬置支架的轻量化设计,在现有的计算机条件下可以很方便的实现。首先,在轻量化分析过程中,一般选取优化设计变量为支架的体积的减少量,然后采用传统的拓扑优化方法,将总体的应变能作为目标函数。在本次后悬置支架的优化分析中,主要采用OptiStruct模块的拓扑优化和形状优化。首先,拓扑优化可以获得一个最佳的结构布局——即最佳的材料分布;然后在这个最优结构布局的基础上按照实际设计需求形成一个新的设计方案,并反馈到CAD软件中,形成新的CAD模型,最后应用更仔细的形状优化工具,同时添加适合铸造的约束条件,得到最有效的细节设计方案。
图(1)代表了该后悬置支架的简单优化设计流程,从最初的模型导入,以及之后的约束条件与目标函数的设定,同时包括制造工艺参数的设定,最后通过形状优化得到的最终设计方案。


根据优化需求,将三维模型进行非安装部位的材料填充导入三维模型

有限元分析论文 有限元分析论文


3.1有限元模型建立
3.1.1后悬置支架原始结构分析
由于驾驶室后悬置系统布置方式比较复杂,整个驾驶室后悬置系统由安装于浮动横梁上的左右各一个橡胶缓冲块支撑,两个悬置支架对称的垂直立于车架大梁上,中间用一弧型横梁连接,在悬置支架的两侧对称的布置两个筒式减震器,而本文所要优化分析的后悬置支架是整个系统中受力最为复杂的关键零件。(www.61k.com)该零件在原始设计中,由于整个机构的复杂性,对产品的性能未能充分把握,在进行设计时只能作定性分析和类比估算,确定实际结构时,选择的安全系数过大,致使设计出来的产品结构过于笨重,粗大,缺乏美观。另外,由于对实际的受力点未能牢牢把握,导致结构材料分布不够均匀,铸造工艺性较差。原始结构见图(2)
五 : 有限元分析课程论文2011
《ANSYS10.0基础及工程应用》考查要求
一、课程考核方式
撰写课程结课论文。(www.61k.com]
二、论文撰写范围
在掌握有限元基本理论及方法的基础上,运用《ANSYS10.0基础及工程应用》课程所学的建模,分网,加载,求解及后处理知识,针对某一你所熟悉的产品、设备或零件进行有限元计算分析。
三、论文撰写要求
1.论文按科技论文的标准格式撰写,包括有题目、作者、单位(班级、学号、联系方式)、摘要(200字左右)、关键词(3—4个)、正文及参考文献(包括作者姓名、文献名、出版社所在地、出版社名、出版时间等),正文引用文献要标出,严禁抄袭。 2.全文字数不少于3000字。
3.参考文献至少5篇。
4.统一以武汉理工大学华夏学院论文纸。
有限元分析论文 有限元分析课程论文2011
有限元分析课程要求
要求:1)个人至少分析3种方案并独立完成(可选择一个模型三种不同方案或三个不同模型的有限
元分析;题目可从上机指南,有限元分析大作业试题中选择或自行选择算例),并将计算结果分析在论文中较详细分析说明(包括几何模型视图、单元模型视图、结果云图,矢量分布图,列表,命令流等及结果分析说明。[www.61k.com])
2)课程论文应包括以下部分:(正文5号字体)
A、 引言;
B、 问题描述及几何建模;
C、 有限元建模(单元选择、节点布置及规模、网格划分方案、载荷及边界条件
处理、求解控制)
D、 计算结果及结果分析(位移分析、应力分析、正确性分析评判,如同一模型则必须进行多方案计算比较,需讨论节点规模增减对精度的影响分析、单元
改变对精度的影响分析、不同网格划分方案、不同结构对结果的影响分析等)
E、 结论
F、 参考文献
3) 12月1日前必须完成,并递交课程论文报告(报告要求打印)。
4) 学生的课程总评成绩由平时成绩(占30%)和期末考查成绩(占70%)两部分构成。平
时成绩中包括出勤、作业、上机操作、学习主动性等。
有限元分析论文 有限元分析课程论文2011
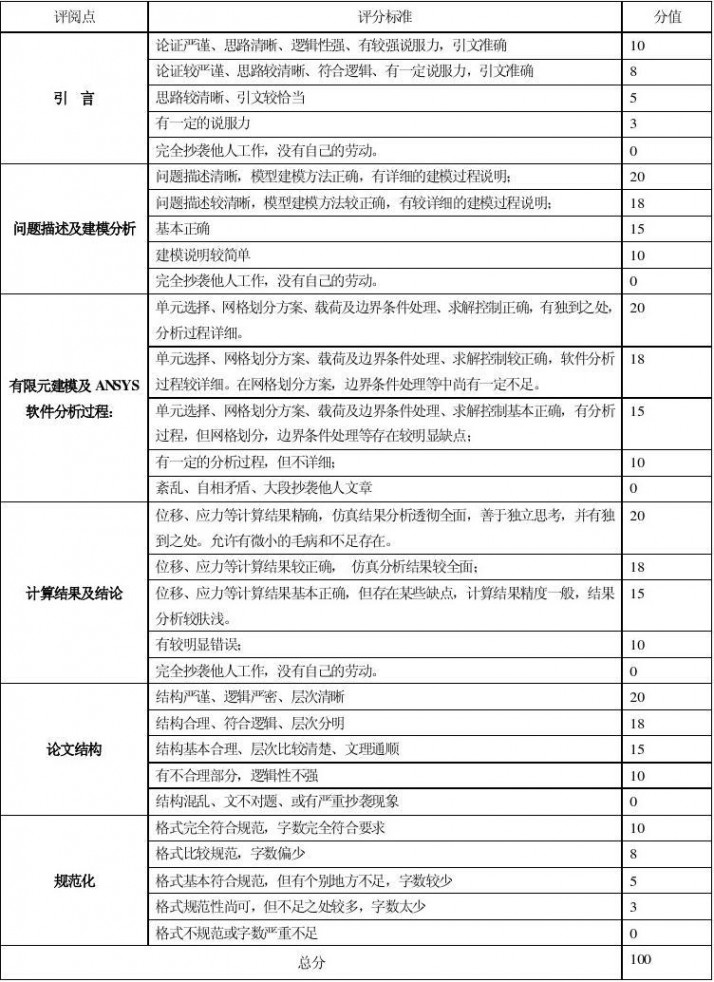
有 限 元 分 析 结 课 报 告 评 分 标 准
有限元分析论文 有限元分析课程论文2011
有 限 元 分 析 大 作 业 试 题
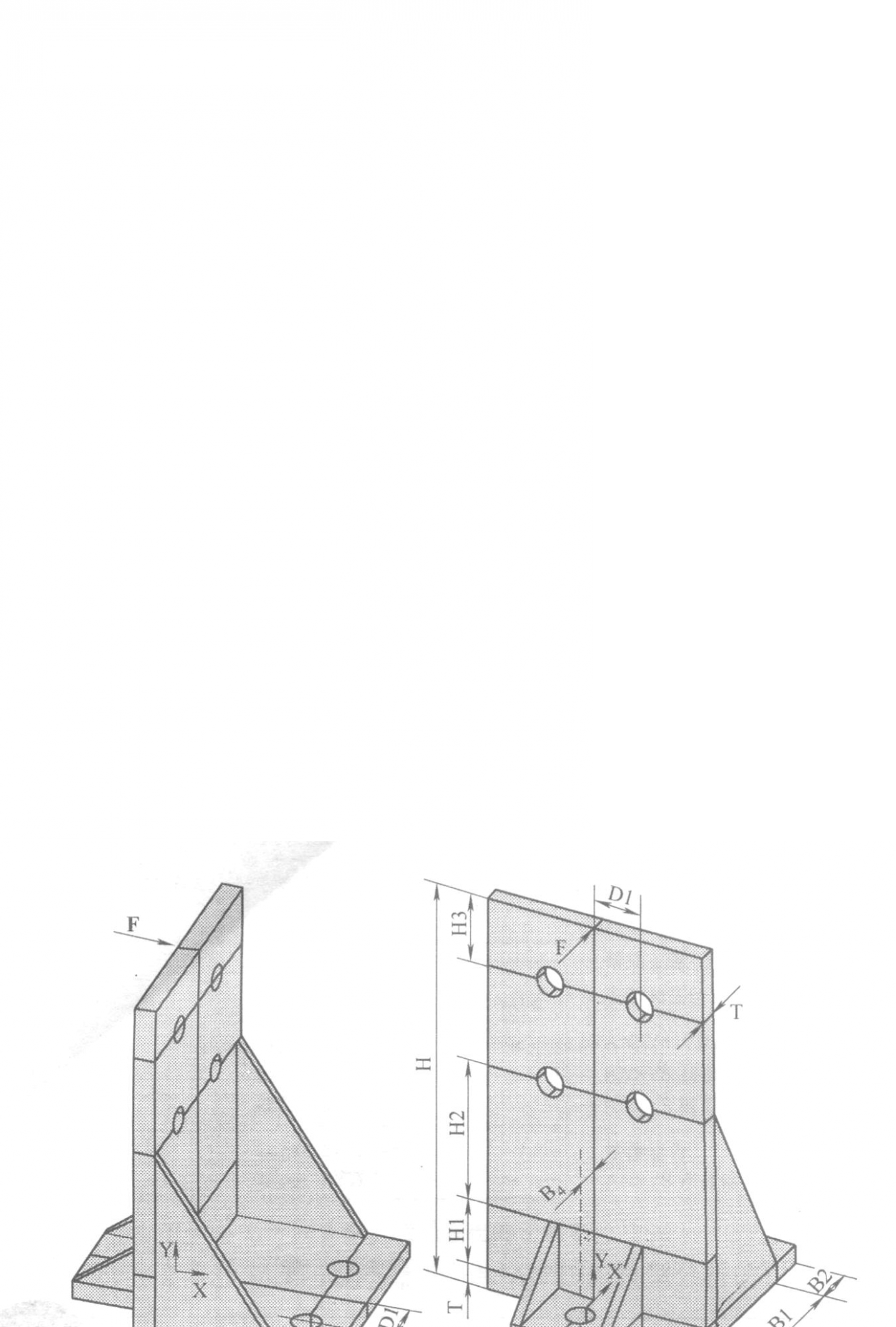
论题1:夹具支架的强度分析
夹具支架的结构如图所示,各部件均有铝制材料制成,工作状态下,底板由三个螺栓固定,在竖向主支撑板上开有定位孔,并在该板顶部侧面承受载荷,根据实际要求,这里仅考虑支架总体的强度,不考虑螺栓连接带来的局部效应,将载荷简化为主支撑板顶部侧面的水平集中力F(如图),大小为10KN。[www.61k.com)夹具底部竖向受到约束,地面螺栓孔边各点不产生水平位移。螺栓和定位孔的半径均为R,主支撑板和底板厚为T,筋板厚为T/2,铝质材料的弹性模量E=76GPa。泊松比V=0.32。进行夹具支架的有限元分析,并对以下几种计算方案进行比较(任选一种):
1. 改变的结构参数或筋板位置,分析结构参数对受力结果的影响(三种)
2. 分别采用自由网格,sweep分网等不同的网格划分策略,分析不同分网策
略对计算结果的影响(三种);
有限元分析论文 有限元分析课程论文2011

论题2 卫星受力分析
如图所示的一个空间卫星,在剪切板与上、下平台外边缘的点上的线位移被约束,沿Z轴以98m/s2 的加速度运行,上、下平台,圆柱面及剪切板的材料为铝,弹性模量E=72.39GPa,泊松比v=0.33,密度ρ=2931kg/m3,适应锥材料为钛,弹性模量E=110.3GPa,泊松比v=0.16,密度ρ=4644kg/m3, 分析卫星的变形及受力情况,并对以下几种计算方案进行比较(任选一种):
1. 改变的结构参数,分析结构参数对受力结果的影响(三种);
2. 分别采用不同的网格划分策略,分析不同分网策略对计算结果的影响(三种);
有限元分析论文 有限元分析课程论文2011
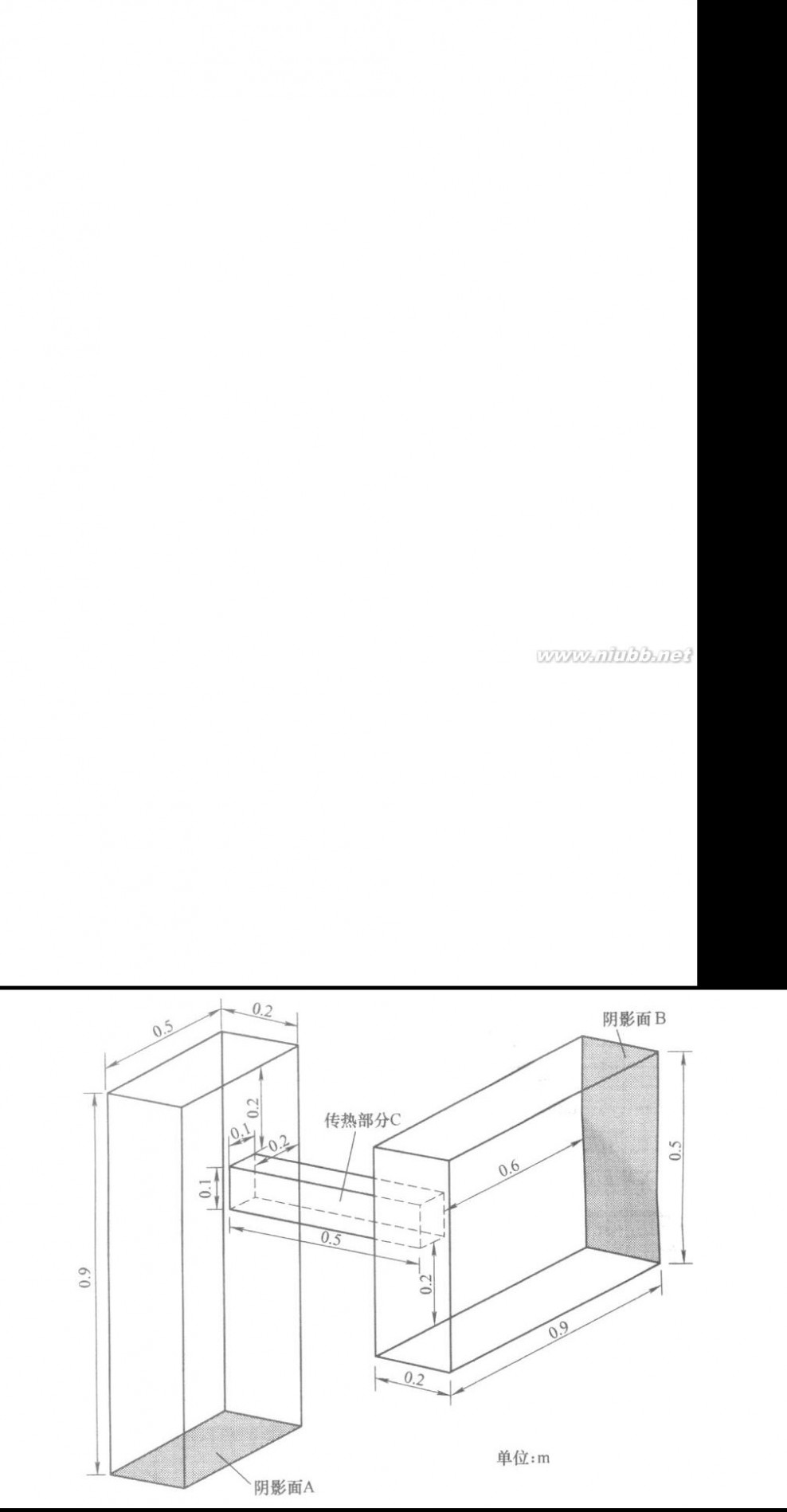
论题3 传热结构的热分析
一传热结构如图所示,两个阴影面上A,B上的温度分别为50°C和135°C,中间传热部分C的环境温度为30°C。(www.61k.com]对流传热系数为20W/(m2?K),该结构各部分为同一材料,其传热系数随温度而变,T=100°C时,传热系数为14.6538 W/(m2?K);T=600°C时,传热系数为22.6087 W/(m2?K);T=1400°C时,传热系数为31.8197W/(m2?K);分析传热结构在温度、对流等载荷作用下的稳态温度分布情况,并改变A,B面位置(三种不同情况);,分析其对温度分布情况的影响
有限元分析论文 有限元分析课程论文2011
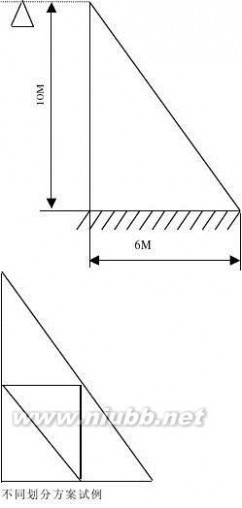
论题4:坝体有限元分析
图示无限长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常应变单元和六节点三角形单元对坝体进行有限元分析,并对以下几种计算方案进行比较:
1) 分别采用相同单元数目的三节点常应变单元和六节点三角
形单元计算;
2) 分别采用不同数量的三节点常应变单元计算;
3) 当选常应变三角单元时,分别采用不同划分方案计算。(www.61k.com)
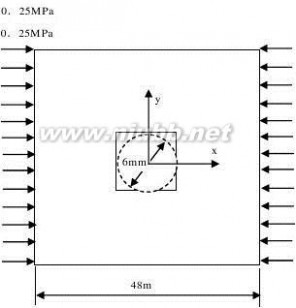
有限元分析论文 有限元分析课程论文2011
61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1