一 : 求函数值域的方法

例析求函数值域的方法

函数的值域是函数三要素之一，求函数的值域是深入学习函数的基础，它常涉及多种知识的综合应用，下面通过例题讲解，多方探寻值域的途径。

一、直接法：（从自变量x的范围出发，推出y?f(x)的取值范围）

例1．求函数y?x?2的值域。 解：因为x?0，所以x?2?2， 所以函数y?x?2的值域为?2,???。

二、配方法（是求二次函数值域的基本方法，如F(x)?af2(x)?bf(x)?c的函数的值域问题，均可使用配方法）

例2．求函数y??x2?4x?2（x?[?1,1]）的值域。

解：y??x2?4x?2??(x?2)2?6，

因为x?[?1,1]，所以x?2?[?3,?1]，所以1?(x?2)?9

所以?3??(x?2)?6?5，即?3?y?5

所以函数y??x2?4x?2（x?[?1,1]）的值域为[?3,5]。

三、分离常数法（分子、分母是一次函数得有理函数，可用分离常数法，此类问题一般也可以利用反函数法）

例4．求函数y?1?x

2x?522的值域。 1

(2x?5)?

2x?577解：因为y?

71?x2x?5????1?， 22x?5

所以1?0，所以y??， 22x?5

1?x

2x?5所以函数y?的值域为{y|y??}。

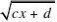
21

四、换元法（运用代数代换，将所给函数化成值域容易确定的另一函数，从而求得原函数的值域，如y?ax?b?a、b、c、d均为常数，且a?0）的函数常用此法求解。

例4

．求函数y?2x?

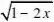
1?t

22解：令t?t?0），则x?，

所以y??t2?t?1??(t?

因为当t?1

212)?254 54，即x?3

8时，ymax?，无最小值。

5所以函数y?2x?(??,]。 4

五、函数的单调性法（确定函数在定义域（或某个定义域的子集）上的单调性，求出函数的值域，形如求函数y?x?k

x?k?0?的值域（0?x?k时为减函数；x?） k时为增函数）

例5

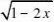
．求函数y?x?

解：因为当x增大时，1?2x随x

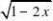
的增大而减少，x的增大而增大，

所以函数y?x?(??,]上是增函数。

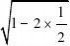
2

1

2121所以y???

，所以函数y?x?(??,]。 21

六、利用有界性(利用某些函数有界性求得原函数的值域)

例6求函数y?x?1

x?122的值域。

解：由函数的解析式可以知道，函数的定义域为R，对函数进行变形可得

(y?1)x??(y?1)，

y?1

y?12因为y?1，所以x2??（x?R，y?1）， 所以?y?1

y?1?0，所以?1?y?1， 所以函数y?x?1

x?122的值域为{y|?1?y?1}

七、数型结合法（函数图像是掌握函数的重要手段，利用数形结合的方法，根据函数图像求得函数值域，是一种求值域的重要方法）

除此之外，还有反函数法（即利用函数和它的反函数的定义域与值域的关系，通过求反函数的定义域而得到原函数的值域）和判别式法（即把函数转化成关于x的二次方程F?x,y??0，通过方程有实根，

，在今后的学习中，会具体讲述。 ??0，从而求得原函数的值域，需熟练掌握一元二次不等式的解法）

二 : 函数的值域怎么求？求方法

的值域怎么求？求方法

---

一．观察法

通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。

例1求函数y=3+√(2－3x) 的值域。

点拨：根据算术平方根的性质，先求出√(2－3x) 的值域。

解：由算术平方根的性质，知√(2－3x)≥0，

故3+√(2－3x)≥3。

∴函数的知域为 .

点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。

本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。

练习：求函数y=[x](0≤x≤5)的值域。（答案：值域为：｛0，1，2，3，4，5｝）

二．反函数法

当函数的反函数存在时，则其反函数的定义域就是原函数的值域。

例2求函数y=(x+1)/(x+2)的值域。

点拨：先求出原函数的反函数，再求出其定义域。

解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数,故函数y的值域为｛y∣y≠1,y∈R｝。

点评：利用反函数法求原函数的定义域的前提条件是原函数存在反函数。这种方法体现逆向思维的思想，是数学解题的重要方法之一。

练习：求函数y=(10x+10-x)/(10x－10-x)的值域。（答案：函数的值域为｛y∣y<－1或y>1｝）

三．配方法

当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域

例3：求函数y=√(－x2+x+2)的值域。

点拨：将被开方数配方成完全平方数，利用二次函数的最值求。

解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2]。此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4]

∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2]

点评：求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。配方法是数学的一种重要的思想方法。

练习：求函数y=2x－5＋√15－4x的值域.(答案:值域为{y∣y≤3})

四．判别式法

若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。

例4求函数y=(2x2－2x+3)/(x2－x+1)的值域。

点拨：将原函数转化为自变量的二次方程，应用二次方程根的判别式，从而确定出原函数的值域。

解：将上式化为（y－2）x2－(y－2)x+(y-3)=0 （＊）

当y≠2时,由Δ=(y－2)2－4（y－2）x+(y－3)≥0，解得：2＜x≤10/3

当y=2时,方程(＊)无解。∴函数的值域为2＜y≤10/3。

点评：把函数关系化为二次方程F(x,y)=0，由于方程有实数解，故其判别式为非负数，可求得函数的值域。常适应于形如y=(ax2+bx+c)/(dx2+ex+f)及y=ax+b±√(cx2+dx+e)的函数。

练习：求函数y=1/(2x2－3x+1)的值域。（答案：值域为y≤－8或y>0）。

五．最值法

对于闭区间[a,b]上的连续函数y=f(x),可求出y=f(x)在区间[a,b]内的极值,并与边界值f(a).f(b)作比较,求出函数的最值,可得到函数y的值域。

例5已知(2x2-x-3)/(3x2+x+1)≤0,且满足x+y=1,求函数z=xy+3x的值域。

点拨：根据已知条件求出自变量x的取值范围，将目标函数消元、配方，可求出函数的值域。

解：∵3x2+x+1＞0，上述分式不等式与不等式2x2-x-3≤0同解，解之得－1≤x≤3/2，又x+y=1，将y=1-x代入z=xy+3x中，得z=-x2+4x(-1≤x≤3/2),

∴z=-(x-2)2+4且x∈[-1,3/2],函数z在区间[-1,3/2]上连续，故只需比较边界的大小。

当x=-1时，z=－5；当x=3/2时，z=15/4。

∴函数z的值域为｛z∣－5≤z≤15/4｝。

点评：本题是将函数的值域问题转化为函数的最值。对开区间，若存在最值，也可通过求出最值而获得函数的值域。

练习：若√x为实数，则函数y=x2+3x-5的值域为 （ ）

A．（－∞，＋∞） B．[－7，＋∞] C．[0，＋∞） D．[－5，＋∞）

（答案：D）。

六．图象法

通过观察函数的图象，运用数形结合的方法得到函数的值域。

例6求函数y=∣x+1∣+√(x-2)2 的值域。

点拨：根据绝对值的意义，去掉符号后转化为分段函数，作出其图象。

解：原函数化为 －2x+1 (x≤1)

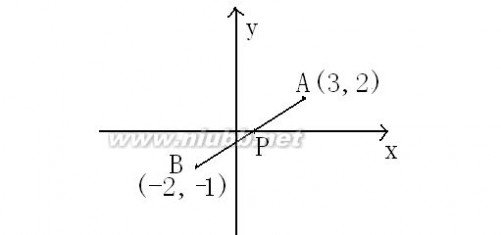
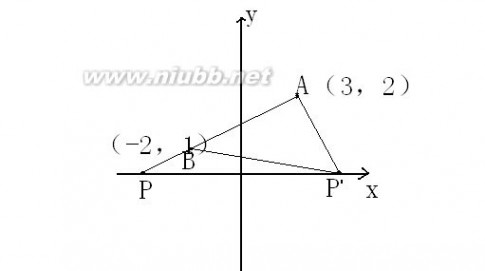
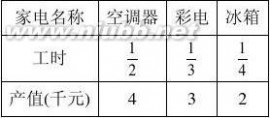
y= 3 (-1

2x-1(x>2)

它的图象如图所示。

显然函数值y≥3,所以，函数值域[3，＋∞]。

点评：分段函数应注意函数的端点。利用函数的图象

求函数的值域，体现数形结合的思想。是解决问题的重要方法。

求函数值域的方法较多，还适应通过不等式法、函数的单调性、换元法等方法求函数的值域。

七．单调法

利用函数在给定的区间上的单调递增或单调递减求值域。

例1求函数y=4x－√1-3x(x≤1/3)的值域。

点拨：由已知的函数是复合函数，即g(x)= －√1-3x,y=f(x)+g(x)，其定义域为x≤1/3，在此区间内分别讨论函数的增减性，从而确定函数的值域。

解：设f(x)=4x,g(x)= －√1-3x ,(x≤1/3),易知它们在定义域内为增函数，从而y=f(x)+g(x)= 4x－√1-3x

在定义域为x≤1/3上也为增函数，而且y≤f(1/3)+g(1/3)=4/3,因此，所求的函数值域为｛y|y≤4/3｝。

点评：利用单调性求函数的值域，是在函数给定的区间上，或求出函数隐含的区间，结合函数的增减性，求出其函数在区间端点的函数值，进而可确定函数的值域。

练习：求函数y=3+√4-x 的值域。(答案：｛y|y≥3｝)

八．换元法

以新变量代替函数式中的某些量，使函数转化为以新变量为自变量的函数形式，进而求出值域。

例2求函数y=x-3+√2x+1 的值域。

点拨：通过换元将原函数转化为某个变量的二次函数，利用二次函数的最值，确定原函数的值域。

解：设t=√2x+1 （t≥0）,则

x=1/2(t2-1)。

于是 y=1/2(t2-1)-3+t=1/2(t+1)2-4≥1/2-4=-7/2.

所以，原函数的值域为｛y|y≥－7/2｝。

点评：将无理函数或二次型的函数转化为二次函数，通过求出二次函数的最值，从而确定出原函数的值域。这种解题的方法体现换元、化归的思想方法。它的应用十分广泛。

练习：求函数y=√x-1 –x的值域。（答案：｛y|y≤－3/4｝

九．构造法

根据函数的结构特征，赋予几何图形，数形结合。

例3求函数y=√x2+4x+5+√x2-4x+8 的值域。

点拨：将原函数变形，构造平面图形，由几何知识，确定出函数的值域。

解：原函数变形为f(x)=√(x+2)2+1+√(2-x)2+22

作一个长为4、宽为3的矩形ABCD，再切割成12个单位

正方形。设HK=x,则ek=2-x,KF=2+x,AK=√(2-x)2+22 ,

KC=√(x+2)2+1 。

由三角形三边关系知，AK+KC≥AC=5。当A、K、C三点共

线时取等号。

∴原函数的知域为｛y|y≥5｝。

点评：对于形如函数y=√x2+a ±√(c-x)2+b(a,b,c均为正数)，均可通过构造几何图形，由几何的性质，直观明了、方便简捷。这是数形结合思想的体现。

练习：求函数y=√x2+9 +√(5-x)2+4的值域。（答案：｛y|y≥5√2｝）

十．比例法

对于一类含条件的函数的值域的求法，可将条件转化为比例式，代入目标函数，进而求出原函数的值域。

例4已知x,y∈R，且3x-4y-5=0,求函数z=x2+y2的值域。

点拨：将条件方程3x-4y-5=0转化为比例式，设置参数，代入原函数。

解：由3x-4y-5=0变形得，(x3)/4=(y-1)/3=k(k为参数)

∴x=3+4k,y=1+3k,

∴z=x2+y2=(3+4k)2+(14+3k)2=(5k+3)2+1。

当k=－3/5时，x=3/5,y=－4/5时，zmin=1。

函数的值域为｛z|z≥1｝.

点评：本题是多元函数关系，一般含有约束条件，将条件转化为比例式，通过设参数，可将原函数转化为单函数的形式，这种解题方法体现诸多思想方法，具有一定的创新意识。

练习：已知x,y∈R，且满足4x-y=0,求函数f(x,y)=2x2-y的值域。（答案：｛f(x,y)|f(x,y)≥1｝）

三 : 求函数值域(最值)的方法大全

求函数值域（最值）的方法大全

函数是中学数学的一个重点,而函数值域(最值)的求解方法更是一个常考点, 对于如何求函数的值域，是学生感到头痛的问题，它所涉及到的知识面广，方法灵活多样，在高考中经常出现，占有一定的地位，因此能熟练掌握其值域(最值)求法就显得十分的重要，求解过程中若方法运用适当，就能起到简化运算过程，避繁就简，事半功倍的作用。［www.61k.com]本文旨在通过对典型例题的讲解来归纳函数值域(最值)的求法，希望对大家有所帮助。

一、值域的概念和常见函数的值域

函数的值域取决于定义域和对应法则，不论采用什么方法球函数的值域均应考虑其定义域.

常见函数的值域：

一次函数y?kx?b?k?0?的值域为R.

?4ac?b2?,???，当a?0时的二次函数y?ax?bx?c?a?0?，当a?0时的值域为??4a?2

?4ac?b2?值域为???,?.， 4a??

反比例函数y?k?k?0?的值域为?y?Ry?0?. x

指数函数y?ax?a?0且a?1?的值域为?yy?0?.

对数函数y?logax?a?0且a?1?的值域为R.

正，余弦函数的值域为??1,1?，正，余切函数的值域为R.

二、求函数值域（最值）的常用方法

1. 直接观察法

适用类型：根据函数图象.性质能较容易得出值域(最值)的简单函数

1的值域 x2?1

1 解：? x2?1?1,?0?2?1 显然函数的值域是：?0,1? x?1 例1、求函数y =

例2、求函数y =2－x的值域。

求函数值域 求函数值域(最值)的方法大全

解：? x≥0 ?－x≤0 2－x≤2

故函数的值域是：[ -∞，2 ]

2 、配方法

适用类型：二次函数或可化为二次函数的复合函数的题型。［www.61k.com)

配方法是求二次函数值域最基本的方法之一。对于形如y?ax2?bx?c?a?0?或F?x??a??f?x????bf?x??c?a?0?类的函数的值域问题，均可用配方法求解. 2

例3、求函数y=x2-2x+5，x?[-1，2]的值域。

解：将函数配方得：y=（x-1）2+4， ? x ?[-1，2]， 由二次函数的性质可知：

当x = 1时，ymin = 4

当x = - 1，时ymax = 8

故函数的值域是：[ 4 ，8 ]

例4

、求函数的值域：y?

解：设???x2?6x?5???

0?，则原函数可化为：y?又因为

???x2?6x?5???x?3??4?4，所以0???

4

?0,2?，所以，y?的值域为?0,2?. 2

3 、判别式法2

适用类型：分子.分母中含有二次项的函数类型，此函数经过变形后可以化为A(y)x2?B(y)x?C(y)?0的形式，再利用判别式加以判断。

2x2?x?2例5、求函数的值域y?2 x?x?1

解：?x2?x?1?0恒成立，?函数的定义域为R.

求函数值域 求函数值域(最值)的方法大全

2x2?x?2 由y?2 得?y?2?x2??y?1?x?y?2?0 。[www.61k.com］ x?x?1

① 当y?2?0即y?2时，3x?0?0,?x?0?R；

② 当y?2?0即y?2时，?x?R时，方程?y?2?x2??y?1?x?y?2?0恒有实

根. ????y?1??4??y?2??0 ?1?y?5且y?2. 22

?原函数的值域为?1,5?.

例6、 求函数y=x+x(2?x)的值域。

解：两边平方整理得：2x2-2（y+1）x+y2=0 （1）

?x?R，?△=4（y+1）2-8y≥0

解得：1-2≤y≤1+2

但此时的函数的定义域由x（2-x）≥0，得：0≤x≤2。

由△≥0，仅保证关于x的方程：2x2-2（y+1）x+y2=0在实数集R有实根，而不能确保其实根在区间[0，2]上，即不能确保方程（1）有实根，由△≥0求出的范围可

13能比y的实际范围大，故不能确定此函数的值域为[，]。可以采取如下方法进一22

步确定原函数的值域。

?0≤x≤2，?y=x+x(2?x) ≥0，

?ymin2?2?22=0，y=1+2代入方程（1），解得：x1=?[0，2]，即当2

2?2?22x1=时，原函数的值域为：[0，1+2]。 2

注：由判别式法来判断函数的值域时，若原函数的定义域不是实数集时，应综合函数的定义域，将扩大的部分剔除。

4、反函数法

适用类型：分子.分母只含有一次项的函数(即有理分式一次型),也可用于其它易反解出自变量的函数类型。

求函数值域 求函数值域(最值)的方法大全

例7、求函数y?2x的值域。［www.61k.com］ x?1

分析与解：由于本题中分子、分母均只含有自变量的一次型,易反解出x,从而便于求出反函数。

y?y2xx反解得x? 即y? 2?yx?12?x

知识回顾：反函数的定义域即是原函数的值域。

故函数的值域为：y?(??,2)?(2,??)。

5 、函数有界性法

直接求函数的值域困难时，可以利用已学过函数的有界性，反客为主来确定函数的值域。

适用类型：一般用于三角函数型，即利用sinx?[?1,1],cosx?[?1,1]等。

ex?1例8、求函数y = x的值域。 e?1

解：由原函数式可得：ex=y?1 y?1

? ex＞0，?y?1＞0 y?1

解得：- 1＜y＜1。

故所求函数的值域为( - 1 , 1 ) .

例9、求函数y = cosx 的值域。 sinx?3

解：由原函数式可得：ysinx-cosx=3y

可化为：y2?1 sinx（x+β）=3y

即 sinx（x+β）=3y

y?12

3y

y?12 ∵x∈R，∴sinx（x+β）∈[-1，1]。即-1≤≤1

求函数值域 求函数值域(最值)的方法大全

解得：-

6 、函数单调性法 2222≤y≤ 故函数的值域为[-，]。(www.61k.com） 4444

适用类型：一般能用于求复合函数的值域或最值。（原理：同增异减）

例10、求函数y?log1(4x?x2)的值域。

2

分析与解：由于函数本身是由一个对数函数（外层函数）和二次函数（内层函数）复合而成，故可令：f(x)??x2?4x(f(x)?0)配方得：

（同增异减）知：y?[?2,??)。 f(x)??(x?2)2?4所以f(x)?（0,4)由复合函数的单调性

例11、 求函数y =

解：令y1=2x?52x?5?log3x?1 （2≤x≤10）的值域 ，y2= log3x?1，则 y1 ， y2在[ 2， 10 ]上都是增函数。 所以y= y1 +y2在[ 2 ，10 ]上是增函数。

当x = 2 时，ymin = 2?3+log312?1= ， 8

当x = 10 时，ymax = 25+log=33。 3

1故所求函数的值域为：[ ，33]。 8

例12、求函数y= x?1-x?1的值域。

解：原函数可化为： y= 2

x?1?x?1

令y1 = x?1，y2= x?1，显然y1 ，y2在[1，+∞）上为无上界的增函数，

所以y= y1 +y2在[1，+∞）上也为无上界的增函数。

所以当x = 1时，y=y1 +y2有最小值2，原函数有最大值

显然y＞0，故原函数的值域为( 0 ,

2]。 22= 2。

求函数值域 求函数值域(最值)的方法大全

7、换元法

通过简单的换元把一个函数变为简单函数，其题型特征是函数解析式含有根式或三角函数公式模型。［www.61k.com）换元法是数学方法中几种最主要方法之一，在求函数的值域中同样发挥作用。

适用类型:无理函数、三角函数（用三角代换）等。

例13、求函数y = x + x?1的值域。

解：令x-1=t，（t≥0）则x=t2+1

13 ∵y=t2+t+1=(t?)2+，又t≥0，由二次函数的性质可知 24

当t=0时，ymin= 1， 当t →0时，y →+∞。

故函数的值域为[ 1 ，+∞）。

例14、求函数y =x+2+?(x?1)2的值域

解：因1-(x?1)2≥0 ，即(x?1)2≤1

故可令x+1=cosβ，β∈[ 0 ，∏] 。

∴y=cosβ+1+?cos2B=sinβ+cosβ+1 =2sin（β+∏/ 4 ）+1

∵0≤β≤∏，0 ≤β+∏/4≤5∏/4

∴ - 2≤sin（β+∏/4）≤1 2

∴ 0 ≤2sin（β+∏/4）+1≤1+2。

故所求函数的值域为[0，1+2]。

x3?x例15、求函数 y=4的值域 2x?2x?1

1?x22x1 解：原函数可变形为：y=-? ?21?x21?x2

1?x22x 可令x=tgβ，则有=sin2β，=cos2β 221?x1?x

求函数值域 求函数值域(最值)的方法大全

11sin2β? cos2β= -sin4β 24

1 当β= k∏/2-∏/8时，ymax=。[www.61k.com） 4

1 当β= k∏/2+∏/8时，ymin= - 4 ∴y=-

而此时tgβ有意义。

11 故所求函数的值域为[-，] 。 44

例16、求函数y=（sinx+1）（cosx+1），x∈[-∏/12∏/2]的值域。 解：y=（sinx+1）（cosx+1）=sinxcosx+sinx+cosx+1

1 令sinx+cosx=t，则sinxcosx=（t2-1） 2

11 y = （t2-1）+t+1= (t?1)2 22

由t=sinx+cosx=2sin（x+∏/4）且x∈[- ∏/12，∏/2] 可得：2≤t≤2 2

2233 ∴当t=时，ymax=+2，当t=时，y=+ 2242

233 故所求函数的值域为[+ ，+2] 。 422

例17、求函数y=x+4+5?x2的值域

解：由5-x≥0 ，可得∣x∣≤

故可令x =cosβ，β∈[0，∏]

y=cosβ+4+5sinβ=sin（β+∏/4）+ 4 ∵ 0 ≤β≤∏， ∴ ∏/4≤β+∏/4≤5∏/4

当β=∏/4时，ymax=4+，当β=∏时，ymin=4-。

故所求函数的值域为：[4-5，4+]。

8 数形结合法

求函数值域 求函数值域(最值)的方法大全

其题型是函数解析式具有明显的某种几何意义，如两点的距离公式直线斜率等等，这类题目若运用数形结合法，往往会更加简单，一目了然，赏心悦目。(www.61k.com)

适用类型:函数本身可和其几何意义相联系的函数类型.

例18、求函数y=(x?2)2+(x?8)2的值域。

解：原函数可化简得：y=∣x-2∣+∣x+8∣

上式可以看成数轴上点P（x ）到定点A（2 ），B（- 8 ）间的距离之和。 由上图可知：当点P在线段AB上时，

y=∣x-2∣+∣x+8∣=∣AB∣=10

当点P在线段AB的延长线或反向延长线上时，

y=∣x-2∣+∣x+8∣＞∣AB∣=10

故所求函数的值域为：[10，+∞）

例19、求函数y=x2?6x?13 + x2?4x?5的值域

2 解：原函数可变形为：y=x?3)?(0?2)+2(x?2)2?(0?1) 2

上式可看成x轴上的点P（x，0）到两定点A（3，2），B（-2 ，-1 ）的距离之和， 由图可知当点P为线段与x轴的交点时，

ymin=∣AB∣= (3?2)2?(2?1)=43， 2

故所求函数的值域为[43，+∞）。

求函数值域 求函数值域(最值)的方法大全

例20、求函数y= x2?6x?13 -x2?4x?5的值域

22 解：将函数变形为：y= (x?3)?(0?2)-x

?2)?(0?1)22

上式可看成定点A（3，2）到点P（x，0 ）的距离与定点B（-2，1）到点P（x，0）的距离之差。[www.61k.com）即：y=∣AP∣-∣BP∣

由图可知：（1）当点P在x轴上且不是直线AB与x轴的交点时，如点P1，则构成△ABP1，根据三角形两边之差小于第三边，

有 ∣∣AP1∣-∣BP1∣∣＜∣AB∣= (3?2)2?(2?1)= 226

即：-26＜y＜26

（2）当点P恰好为直线AB与x轴的交点时，有

∣∣AP∣-∣BP∣∣= ∣AB∣= 26。

综上所述，可知函数的值域为：（-26，-26]。 注：由例17，18可知，求两距离之和时，要将函数式变形，使A，B两点在x 轴的两侧，而求两距离之差时，则要使两点A ，B在x轴的同侧。

如：例17的A，B两点坐标分别为：（3 ，2 ），（- 2 ，- 1 ），在x轴的同侧； 例18的A，B两点坐标分别为：（3 ，2 ），（2 ，- 1 ），在x轴的同侧。 例21、求函数y?3?sinx的值域. 2?cosx

B x 分析与解:看到该函数的形式,我们可联想到直线中已知两点求直线的斜率的公式

k?y2?y1,将原函数视为定点(2,3)到动点(cosx,sinx)的斜率,又知动点(cosx,sinx)x2?x1

满足单位圆的方程,从而问题就转化为求点（2，3）到单位圆连线的斜率问题,作出图形观察易得的最值在直线和圆上点的连线和圆相切时取得,从而解得:

求函数值域 求函数值域(最值)的方法大全

y?[6?236?2,] 33

9 、不等式法

适用类型：能利用几个重要不等式及推论来求得最值。（www.61k.com]（如：a2?b2?2ab,a?b?2ab）

其题型特征解析式是和式时要求积为定值，解析式是积时要求和为定值，不过有时须要用到拆项、添项和两边平方等技巧。

例22、 求函y=（sinx +1/sinx）+（cosx+1/cosx）的值域

解：原函数变形为：

y=（sinx+cosx）+1/sinx+1/cosx

= 1+ 2222csc

2x+secx= 3+tgx+ctgx 222

当且仅当tgx=ctgx，即当x=k∏±∏/4时（k∈z），等号成立。

故原函数的值域为：[ 5，+∞）。

例23、求函数y=2sinxsin2x的值域

解：y=2sinxsinxcosx=4sinxcosx 2

y2=16sinx

24cos22x 2=8sinxsinx（2-2sinx）

≤8（sinx+sinx+2-

=8[（sin

=64 27

22222sin2x） 2x+sinx+2- 2sin2x）/3]3 当且当sinx=2-2sinx，即当sinx=时，等号成立。

由y≤283864，可得：-≤y≤ 9927

求函数值域 求函数值域(最值)的方法大全

故原函数的值域为：[-8383，）。（www.61k.com) 99

4的最值，并指出f(x)取最值时x的值。 x2

44分析与解：因为f(x)?8x?2?4x?4x?2可利用不等式a?b?c?abc即：xx例24、当x?0时，求函数f(x)?8x?

f(x)?34x?4x?44所以当且仅当即x?1时取”=”当x?1时f(x)f(x)?124x?x2x2

取得最小值12。

x2y2y2x2

例25、双曲线2?2?1的离心率为e1，双曲线2?2?1的离心率为e2，则e1?e2abba

的最小值是（ ）。

A 22 B 4 C 2 D

分析与解：根据双曲线的离心率公式易得：e1?e2?2 a2?b2a2?b2

?，我们知道ab

a2?b2a2?b2

x?y?2xy所以e1?e2?2?（当且仅当abaa2?b2时取“=”）而b

a2?b2?2ab故e1?e2?22（当且仅当a?b时取“=”）所以(e1?e2)min?22。

10、导数法

设函数f?x?在?a,b?上连续，在?a,b?上可导，则f?x?在?a,b?上的最大值和最小值为f?x?在?a,b?内的各极值与f?a?，f?b?中的最大值与最小值。

要求三次及三次以上的函数的最值,以及利用其他方法很难求的函数似的最值,通常都用该方法。导数法往往就是最简便的方法,应该引起足够重视。

例26、求函数f?x??x3?3x2?6x?2,x???1,1?的最大值和最小值。

解: f'?x??3x2?6x?6,令f'?x??0,方程无解.

?f'?x??3x2?6x?6?3?x?1??3?0 ?函数f?x?在x???1,1?上是增函数. 2

故当x??1时, fmin?x??f??1???12，当x?1时, fmax?x??f?1??2

求函数值域 求函数值域(最值)的方法大全

例27、求函数f(x)?1的最值. 2x?2x?2

解析: 函数f(x)是定义在一个开区间???，???上的可导函数, 令f'(x)??2x?2?0 2(x?2x?2)

得f(x)的唯一驻点x??1即为最点.

x??1时，f'(x)?0，函数递增,

x??1时，f'(x)?0，函数递减,

故f(x)有最大值f(?1)?1.

【说明】 本函数是二次函数的复合函数，用配方法求最值也很简便. f(x)?1?1,等号成立条件是x??1. 2(x?1)?1

注：最值寻根的导数判定

若定义在一个开区间上的函数y?f(x)有导函数f?(x)?g(x)存在，那么f(x)是否有最值的问题可转化为f(x)的导函数g(x)是否有最根的问题来研究：

（1）若导函数g(x)无根，即g(x)?0，则f(x)无最值；

（2）若导函数g(x)有唯一的根x0，即f'(x0)?0，则f(x)有最值f(x0).此时，导函数f?(x)的根x0即是函数f(x)最根x0.

（3）若导函数g(x)有多个的根，则应从多个驻点中依次判定极点、最点的存在性.

11、多种方法综合运用

例28、求函数y=x?2的值域 x?3

解：令t=x?2 （t≥0），则x+3=t2+1

求函数值域 求函数值域(最值)的方法大全

（1） 当t＞0时，y=

所以0＜y≤1。（www.61k.com） 211≤， 当且仅当t=1，即x=-1时取等号 2t?1t?1/t2t=

1（2） 当t=0时，y=0。综上所述，函数的值域为：[0，]。 2

注：先换元，后用不等式法。

例29、求函数y=1?x?2??1?2x?x

424234的值域。 221?x)+x 解：y=+=(1?2x?x1?2x?x1?x21?x1?2?224x?2342

令x=tg?1?x=2?，x=1sin， ，则(?)cos221?x21?222x

∴y=cos?+

=-(sin2112sin?=-sin?+ sin?+1 2221??)4+17 16

117∴当sin?=时，ymax=。当sin?=-1时，ymin=-2。 416

?17此时tg都存在，故函数的值域为：［－2，］。 216

注：此题先用换元法。后用配方法，然后再运用sin?的有界性。

总之，在具体求某个函数的值域时，首先要仔细、认真观察其题型特征，然后再选择恰当的方法，一般优先考虑直接法，函数单调性法和基本不等式法，然后才考虑用其他各种特殊方法。

学生巩固练习

11 (x≤－)的值域是( ) 2x

77332A(－∞,－] B［－,+∞) C［,+∞) D(－∞,－2］ 24421 函数y=x2+

求函数值域 求函数值域(最值)的方法大全

2 函数y=x+?2x的值域是( )

A (－∞,1] B (－∞,－1] C R D ［1,+∞)

3 一批货物随17列货车从A市以V千米/小时匀速直达B市，已知两地铁路线长400千米，为了安全，两列货车间距离不得小于(V2)千米 ，那么这批物资全部运20

到B市，最快需要_________小时(不计货车的车身长)

4 设x1、x2为方程4x2－4mx+m+2=0的两个实根，当m=_________时，x12+x22有最小值_________

5 某企业生产一种产品时，固定成本为5000元，而每生产100台产品时直接消耗成本要增加2500元，市场对此商品年需求量为500台，销售的收入函数为R(x)=5x－x2(万元)(0≤x≤5),其中x是产品售出的数量(单位 百台)

(1)把利润表示为年产量的函数；

(2)年产量多少时，企业所得的利润最大？

(3)年产量多少时，企业才不亏本？

6 已知函数f(x)=lg［(a2－1)x2+(a+1)x+1］

(1)若f(x)的定义域为(－∞,+∞)，求实数a的取值范围；

(2)若f(x)的值域为(－∞,+∞),求实数a的取值范围

7 某家电生产企业根据市场调查分析，决定调整产品生产方案，准备每周(按120个工时计算)生产空调器、彩电、冰箱共360台，且冰箱至少生产60台 已知生产家电产品每台所需工时和每台产值如下表

12问每周应生产空调器、彩电、冰箱各多少台，才能使产值最高？最高产值是多少？(以千元为单位)

8 在Rt△ABC中，∠C=90°，以斜边AB所在直线为轴将△ABC旋转一周生成两个圆锥，设这两个圆锥的侧面积之积为S1，△ABC的内切圆面积为S2，记BC?CA=x AB

求函数值域 求函数值域(最值)的方法大全

(1)求函数f(x)=S1的解析式并求f(x)的定义域 S2

(2)求函数f(x)的最小值

参考答案

1 解析 ∵m1=x2在(－∞,－）上是减函数，m2=在(－∞,－）上是减函数，∴y=x2+11在x∈(－∞,－)上为减函数, 2x

117∴y=x2+ (x≤－)的值域为［－，+∞) 24x121x12

答案 B

1?t22 解析 令?2x=t(t≥0),则x= 2

11?t2∵y=+t=－ (t－1)2+1≤1 22

∴值域为(－∞,1]

答案 A

3 解析 t=

答案 8

m?2, 4

m?2117∴x12+x22=(x1+x2)2－2x1x2=m2－=(m－)2－, 2416400V240016V+16×()/V=+≥2=8 VV204004 解析 由韦达定理知 x1+x2=m,x1x2=

又x1,x2为实根，∴Δ≥0 ∴m≤－1或m≥2，

17在区间(－∞,1）上是减函数，在［2，+∞)上是增函数，又抛物16

1线y开口向上且以m=为对称轴 故m=1时， 4

1ymin= 2

1答案 －1 2y=(m－)2－14

5 解 (1）利润y是指生产数量x的产品售出后的总收入R(x)与其总成本C(x)?之差，由题意，当x≤5时，产品能全部售出，当x>5时，只能销售500台，所以

求函数值域 求函数值域(最值)的方法大全

12?125x?x?(0.5?0.25x)(0?x?5)????4.75x?x?0.5(0?x?5)2y=? ??21?(5?5??52)?(0.5?0.25x)(x?5)??12?0.25x (x?1)?2?

1b(2）在0≤x≤5时，y=－x2+4 75x－0 5,当x=－=4 75(百台）时，ymax=10 22a

78125(万元），当x>5(百台）时，y＜12－0 25×5=10 75(万元），?

所以当生产475台时，利润最大 ?

?0?x?5?x?5?(3）要使企业不亏本，即要求?12 或?x?4.75x?0.5?0?12?0.25x?0??2

解得5≥x≥4 75－21.5625≈0 1(百台）或5＜x＜48(百台）时，即企业年产量在10台到4800台之间时，企业不亏本

6 解 (1）依题意(a2－1）x2+(a+1)x+1>0对一切x∈R恒成立，当a2－1≠0时，?a?1或a??12??a?1?0?其充要条件是?， ,即?522a?或a??1????(a?1)?4(a?1)?0?3?

∴a＜－1或a>

又a=－1时，f(x)=0满足题意，a=1时不合题意

故a≤－1或a>为所求

(2）依题意只要t=(a2－1)x2+(a+1)x+1能取到(0，+∞）上的任何值，则f(x)的值域

?a2?1?05为R，故有?,解得1＜a≤,又当a2－1=0即a=1时，t=2x+1符合题意而a=－3???05353

1时不合题意，∴1≤a≤为所求

7 解 设每周生产空调器、彩电、冰箱分别为x台、y台、z台，由题意得 x+y+z=360?

① 53111x?y?z?120 234 ② ③? x>0,y>0,z≥60

假定每周总产值为S千元，则S=4x+3y+2z,在限制条件①②③之下，为求目标函数S的最大值，由①②消去z,得

求函数值域 求函数值域(最值)的方法大全

y=360－3x ④

⑤ 将④代入①得 x+(360－3x)+z=360,∴z=2x

∵z≥60,∴x≥30 ⑥

再将④⑤代入S中，得S=4x+3(360－3x)+2·2x,即S=－x+1080

由条件⑥及上式知，当x=30时，产值S最大，最大值为 S=－30+1080=1050(千元）

得x=30分别代入④和⑤得y=360－90=270,z=2×30=60

∴每周应生产空调器30台，彩电270台，冰箱60台，才能使产值最大，最大产值为1050千元

8 解 (1）如图所示 设BC=a,CA=b,AB=c,则斜边AB上的高h=

∴S1=πah+πbh=

∴f(x)=?abc(a?b),S2??(a?b?c2),, 2C

bab, cS14ab(a?b) ?S2c(a?b?c)2 ① ?a?b?a?b?cx?x????又?c c22ab?(x?1)?a2?b2?c2?2??acB

2(x2?x)代入①消c，得f(x)= x?1

在Rt△ABC中，有a=csinA,b=ccosA(0＜A＜

x=?),则 2a?b?=sinA+cosA=2sin(A+) ∴1＜x≤2 c4

2(x2?x)2(2)f(x)=?2[(x?1)?] +6, x?1x?1

2设t=x－1,则t∈(0, 2－1),y=2(t+)+6 t

在(0，2－1]上是减函数，

∴当x=(2－1)+1=2时，f(x)的最小值为62+8

四 : 求函数值域的11种必考方法，你学会了吗？

小数老师说

函数，是高中数学中很重要的一部分内容，很多同学也为函数值域的求法感到头痛。(www.61k.com）今天我就给大家分享一下，高中数学中函数值域的11种求法。只要同学们熟练掌握了这些求法，便能轻轻松松地应对高中函数了。

更多内容关注高中数学微信公众号！

61阅读提醒您本文地址：

本文标题：求函数值域的方法-求函数值域的方法
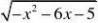
本文地址： http://www.61k.com/1072492.html