一 : 环境空气质量标准编制说明
二 : 去年2月29日,我国发布了新修订的《环境空气质量标准》
去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在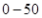 为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为 为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为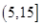 , ,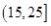 , ,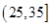 , ,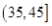 ,由此得到样本的空气质量指数频率分布直方图,如图. ,由此得到样本的空气质量指数频率分布直方图,如图.(1) 求 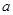 的值; 的值;(2) 根据样本数据,试估计这一年度的空气质量指数的平均值;(注:设样本数据第 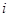 组的频率为 组的频率为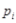 ,第 ,第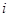 组区间的中点值为 组区间的中点值为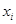 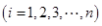 ,则样本数据的平均值为 ,则样本数据的平均值为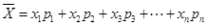 .) .)(3) 如果空气质量指数不超过  ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取 ,就认定空气质量为“特优等级”,则从这一年的监测数据中随机抽取 天的数值,其中达到“特优等级”的天数为 天的数值,其中达到“特优等级”的天数为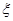 ,求 ,求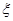 的分布列和数学期望. 的分布列和数学期望.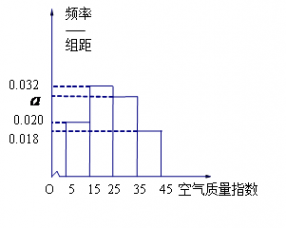 |
(1)0.03;(2)24.6;(3)分布列详见解析, . . |
试题分析:本题主要考查频率分布直方图、由样本估计总体求平均值、二项分布、离散型随机变量的分布列和数学期望等基础知识,考查学生的分析问题解决问题的能力、计算能力、转化能力.第一问,利用频率分布直方图中长方形的高=频率/组距,而所有频率之和为1,来计算a的值;第二问,根据样本数据,估计总体的平均值的计算公式为:频率分布直方图中,每一个长方形的中点×高×组距,得到的数据之和即为平均值;第三问,利用频率分布直方图先得到 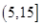 内的频率,即“特优等级”的概率值,通过分析题意可知随机变量 内的频率,即“特优等级”的概率值,通过分析题意可知随机变量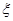 服从二项分布,利用 服从二项分布,利用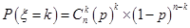 计算出每一种情况的概率,再利用 计算出每一种情况的概率,再利用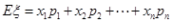 计算出数学期望 计算出数学期望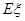 . .试题解析:(1) 由题意,得 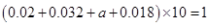 ,1分 ,1分解得 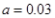 .2分 .2分(2) 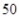 个样本中空气质量指数的平均值为 个样本中空气质量指数的平均值为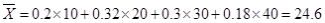 3分 3分由样本估计总体,可估计这一年度空气质量指数的平均值约为 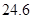 . 4分 . 4分(3)利用样本估计总体,该年度空气质量指数在 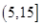 内为“特优等级”, 内为“特优等级”,且指数达到“特优等级”的概率为 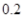 ,则 ,则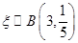 .5分 .5分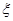 的取值为 的取值为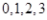 ,6分 ,6分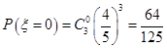 , , , , , ,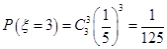 .10分 .10分∴ 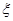 的分布列为: 的分布列为:
∴ 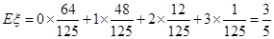 .12分 .12分(或者 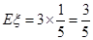 ) ) |
考点:
考点名称:离散型随机变量的期望与方差数学期望的定义:
称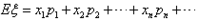 为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
为ξ的数学期望或平均数,均值,数学期望又简称为期望,它反映了随机变量取值的平均水平。
方差的定义:
称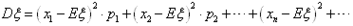 为ξ的均方差,简称为方差,
为ξ的均方差,简称为方差,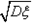 叫做随机变量ξ的标准差,记作:
叫做随机变量ξ的标准差,记作: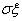 。
。
期望与方差的性质:
(1)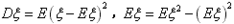 ;
;
(2)若η=aξ+b,则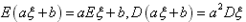 ;
;
(3)若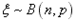 ,则
,则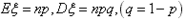 ;
;
(4)若ξ服从几何分布,则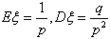 。
。
求均值(数学期望)的一般步骤:
(1)首先判断随机变量是否服从二点分布、二项分布或超几何分布,若服从,则直接用公式求均值.(2)若不服从特殊的分布,则先求出随机变量的分布列,再利用公式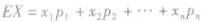 求均值。
求均值。
方差的求法:
(1)若随机变量X服从二点分布或二项分布,则直接利用方差公式可求.
(2)若随机变量X不服从特殊的分布时,求法为:
三 : 空气与环境
空气与环境61阅读| 精彩专题| 最新文章| 热门文章| 苏ICP备13036349号-1